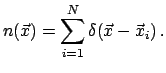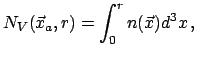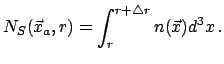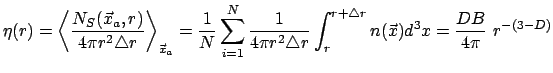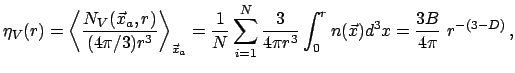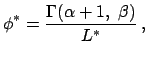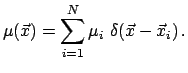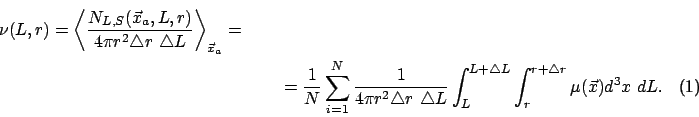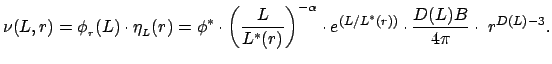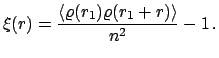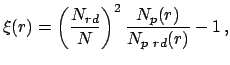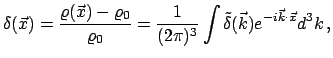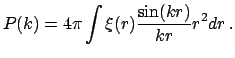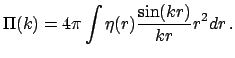Крупномасштабная структура распределения вещества во Вселенной

П. А. Тараканов
Санкт-Петербургский государственный университет
| Достаточно давно было обнаружено, что распределение вещества во Вселенной на больших масштабах существенно неоднородно. В то же время характерные параметры неоднородностей и сейчас активно исследуются и обсуждаются. Поскольку возможный механизм возникновения неоднородностей должен быть теснейшим образом связан с эволюцией Вселенной в целом, совокупность данных о крупномасштабной структуре распределения вещества в пространстве является одним из существенных наблюдательных оснований современной космологии. |
When SDSS data was released in 2004, physicists David Hogg of New York University and Daniel Eisenstein of the University of Arizona, both in the US, published an analysis of 55,000 luminous red galaxies suggesting that the fractal pattern smoothed out at scales over 200 million light years.
Оглавление
- 1. Введение
- 2. Наблюдательные данные
- 3. Способы описания структуры
- 4. Методы анализа структуры
- 5. Современное состояние
- Литература
1. Введение
Достаточно давно было обнаружено, что распределение вещества во Вселенной на
больших масштабах
(![]() Мпк)
существенно неоднородно. В то же время
характерные параметры неоднородностей и сейчас активно исследуются и
обсуждаются. Поскольку возможный механизм возникновения неоднородностей должен
быть теснейшим образом связан с эволюцией Вселенной в целом, совокупность данных
о крупномасштабной структуре распределения вещества в пространстве является
одним из существенных наблюдательных оснований современной космологии.
Мпк)
существенно неоднородно. В то же время
характерные параметры неоднородностей и сейчас активно исследуются и
обсуждаются. Поскольку возможный механизм возникновения неоднородностей должен
быть теснейшим образом связан с эволюцией Вселенной в целом, совокупность данных
о крупномасштабной структуре распределения вещества в пространстве является
одним из существенных наблюдательных оснований современной космологии.
Методы изучения пространственного распределения вещества можно разделить на три основных класса.
- Непосредственные измерения пространственных координат (небесных координат и красных смещений) светящихся объектов (главным образом галактик) и статистическая обработка соответствующих наблюдательных данных. Этот метод в настоящее время позволяет исследовать распределение светящегося вещества на масштабах до сотен Мпк.
- Анализ эффектов гравитационного линзирования, позволяющий изучать
структуру скрытой массы, проявляющей себя лишь в гравитационном
взаимодействии. Хотя объем данных по гравитационным линзам к настоящему
времени не очень велик, этот метод позволяет анализировать распределение
скрытой массы на масштабах
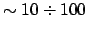 Мпк.
Мпк.
- Численное моделирование гравитационного скучивания в рамках задачи
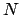 тел.
Этот метод позволяет изучать характер эволюции крупномасштабной структуры, что
дает возможность получать информацию об особенностях структуры в эпохи,
недоступные непосредственным наблюдениям.
тел.
Этот метод позволяет изучать характер эволюции крупномасштабной структуры, что
дает возможность получать информацию об особенностях структуры в эпохи,
недоступные непосредственным наблюдениям.
2. Наблюдательные данные
Анализ распределения светящегося вещества - галактик, скоплений, сверхскоплений - возможен только при наличии достаточно полных наблюдательных внегалактических обзоров.
Первые данные о крупномасштабной структуре были получены путем визуального
исследования пластинок Паломарского обзора неба. В результате Эйблом был
составлен первый каталог скоплений галактик, покрывавший небо в области
![]() .
Позже каталог был распространен на южное небо, итоговый его вариант включает
4074 скопления.
.
Позже каталог был распространен на южное небо, итоговый его вариант включает
4074 скопления.
До появления возможности массовых измерений красных смещений внегалактических объектов обзоры галактик содержали небесные координаты и более или менее полные данные фотометрических наблюдений. В этот период заключения о распределении материи основывались на подсчетах галактик до определенной звездной величины. Такие данные, полученные до 80-х гг. XX в., давали возможность лишь косвенно оценить параметры крупномасштабной структуры, хотя именно по ним был установлен сам факт наличия структуры и предложен сценарий иерархического скучивания.
В последнее десятилетие создано (или создается) несколько крупных пространственных внегалактических обзоров, содержащих данные о небесных координатах и красных смещениях объектов, а также прочие характеристики объектов. Пространственные обзоры можно разделить на широкоугольные (покрывающие большой телесный угол на небесной сфере), обзоры, протяженные только по одной из угловых координат, и «карандашные» обзоры, в которых приведены данные об объектах, угловые координаты которых находятся в малой области на небесной сфере. Каждый из типов пространственных обзоров эффективно выполняет определенные задачи. Например, карандашные обзоры могут помочь заглянуть в очень удаленные области наблюдаемой Вселенной, а широкоугольные обзоры, получаемые до много меньших глубин, позволяют применять все разнообразие статистических методов.
Фотометрический обзор галактик до величины
![]() ,
выполненный Цвикки, послужил базой для трехмерного обзора CfA1, содержащего
красные смещения, полученные в Гарвардском центре астрофизики (Harvard Center
for Astrophisics). Широкоугольный обзор CfA1 впервые показал, что распределение
объектов во Вселенной согласуется с представлениями о ячеистой структуре,
определяющими элементами которой являются большие пустоты и обрамляющие их
«стенки» из галактик (сверхскопления). На карте обзора CfA1 выделяется
образование, названное Великой Стеной (Great Wall).
,
выполненный Цвикки, послужил базой для трехмерного обзора CfA1, содержащего
красные смещения, полученные в Гарвардском центре астрофизики (Harvard Center
for Astrophisics). Широкоугольный обзор CfA1 впервые показал, что распределение
объектов во Вселенной согласуется с представлениями о ячеистой структуре,
определяющими элементами которой являются большие пустоты и обрамляющие их
«стенки» из галактик (сверхскопления). На карте обзора CfA1 выделяется
образование, названное Великой Стеной (Great Wall).
Расширением этого обзора стал каталог CfA2. Вместе с южным обзором галактик
SSRS2, выполненным также до величины ![]() , он содержит сведения (в
том числе о красных смещениях) для примерно 20000 галактик.
, он содержит сведения (в
том числе о красных смещениях) для примерно 20000 галактик.
Сейчас для составления пространственных обзоров применяются специализированные телескопы («z-машины»), ориентированные для массового измерения красных смещений объектов.
В обзор галактик 2dFGRS (www.mso.anu.edu.au/2dFGRS) входит
221414 галактик. Для получения красных смещений использовался мультиобъектный
спектрограф с полем ![]() , способный отснять за одну экспозицию 400 спектров.
Основой обзора послужил фотометрический каталог APM. Для обзора 2dFGRS были
отобраны все галактики, которые после коррекции видимых величин за поглощение
оказались ярче
, способный отснять за одну экспозицию 400 спектров.
Основой обзора послужил фотометрический каталог APM. Для обзора 2dFGRS были
отобраны все галактики, которые после коррекции видимых величин за поглощение
оказались ярче ![]() . Основная область на небесной сфере, покрытая обзором
2dFGRS, - две полосы по склонению:
. Основная область на небесной сфере, покрытая обзором
2dFGRS, - две полосы по склонению: ![]() около южного
галактического полюса и область
около южного
галактического полюса и область ![]() в северной галактической полусфере.
Дополнительно отсняты галактики в 99 случайно расположенных полях в
высокоширотной области южной галактической полусферы. Обзор покрывает около
в северной галактической полусфере.
Дополнительно отсняты галактики в 99 случайно расположенных полях в
высокоширотной области южной галактической полусферы. Обзор покрывает около ![]() квадратных градусов и имеет медианную глубину
квадратных градусов и имеет медианную глубину ![]() .
.
Главным ограничением обзора 2dFGRS является специфическая форма его
объема - выборка покрывает две узкие полосы на небесной сфере, поэтому
максимальный радиус шара, полностью содержащегося в выборке, не превышает
100 Мпк. Следовательно, этот обзор не даст надежной информации о больших
масштабах, хотя глубина выборки достигает ![]() .
.
Самый большой современный проект - Sloan Digital Sky Survey (SDSS,
www.sdss.org). Обзор красных смещений галактик покроет все
северное небо и полосу на южном небе. Будут получены спектры для всех галактик в
этих областях до ![]() и для активных ядер до
и для активных ядер до ![]() , что даст возможность
исследовать крупномасштабную структуру на масштабах до 1 Гпк. Общее
количество галактик с полученными в рамках проекта спектрами будет превышать
, что даст возможность
исследовать крупномасштабную структуру на масштабах до 1 Гпк. Общее
количество галактик с полученными в рамках проекта спектрами будет превышать
![]() .
.
Сводка данных о других каталогах, используемых для изучения крупномасштабной структуры, приводится в табл. 1.
| Таблица. Основные характеристики каталогов красных смещений галактик. (Ω – телесный угол, покрываемый каталогом на небесной сфере (стерад), Rd – глубина каталога (Мпк), Rs – радиус максимальной сферы, которая может быть вписана в объем каталога (Мпк)). Расстояния даны для H0=60 км/(с.Мпк) | ||||||||||||||||||||||||||||||||||||||||||||
|
3. Способы описания структуры
При описании крупномасштабной структуры сейчас, как правило, используется два типа моделей: однородная модель с флуктуациями плотности, а также фрактальная модель. Обе эти модели обладают как достоинствами, так и недостатками.
Однородное распределение, на которое накладываются флуктуации плотности конечной амплитуды, удобно для аналитического описания структуры. В то же время реально наблюдаемые особенности структуры - ее самоподобие в значительном интервале масштабов, отсутствие надежно выделяемых центров концентрации и т. п. - лучше описываются в рамках фрактальной модели. В последние годы фрактальные модели достаточно широко используются как в астрофизике, так и в физике вообще. Для многих систем фрактальные модели являются простейшими способами описания структуры, чем, в частности, объясняется их популярность. В то же время принципиальная неаналитичность фрактальных моделей создает значительные трудности при описании процессов, приводящих к формированию структур такого рода. Более подробно общие свойства фрактальных моделей рассматривались в лекции, прочитанной на XXXII Школе в 2003 г.
Понятие плотности жидкости/газа, обычно используемое в гидродинамике, содержит предположение о том, что существует значение плотности, не зависящее от величины элемента объема. Тогда можно определить плотность как функцию пространственных координат (как правило, непрерывную). В задаче анализа флуктуаций функция плотности может быть реализацией стохастического процесса, для которого определены обычные моменты - среднее, дисперсия и т. д. В частности, это может быть и дискретный процесс, содержащий конечное число точек, например, пуассоновский процесс.
В случае фрактальных структур понятия плотности числа частиц в точке не
существует, так как в каждом элементе объема структуры содержится иерархия
кластеров и значение концентрации существенно зависит от величины элемента
объема. Для описания непрерывной иерархии скучивания, являющейся новой
характеристикой процесса, необходимо ввести специальную независимую
переменную - радиус области (![]() ), в которой производится подсчет частиц. При
этом число частиц самоподобной структуры растет по степенному закону
), в которой производится подсчет частиц. При
этом число частиц самоподобной структуры растет по степенному закону
где
Рассмотрим дискретный стохастический процесс, реализации которого
представляют совокупности частиц, расположенных в случайно выпавших положениях
![]() ,
так что реализованная плотность числа частиц
,
так что реализованная плотность числа частиц ![]() дается выражением
дается выражением
Если стохастический процесс является фрактальным, то для его описания необходимо рассмотреть дополнительную «фрактальную» переменную
и
При переходе от реализации к реализации эти величины испытывают флуктуации,
после осреднения которых по множеству реализаций остается зависимость от
масштаба ![]() . В случае эргодических процессов осреднение по реализациям можно
заменить осреднением по множеству точек одной реализации. Определим условную
концентрацию стохастического фрактального процесса в виде
. В случае эргодических процессов осреднение по реализациям можно
заменить осреднением по множеству точек одной реализации. Определим условную
концентрацию стохастического фрактального процесса в виде
и объемную условную концентрацию в виде
где
называется фрактальной коразмерностью структуры.
Принципиально важным свойством условной концентрации является то, что для
процессов с конечным масштабом фрактальности, после которого распределение
частиц становится однородным, статистики (5) и (6) выходят
на постоянное значение, что соответствует равенству ![]() для однородных структур.
Таким образом, метод условной концентрации является мощным инструментом поиска
границы перехода от режима фрактальной кластеризации к однородности.
для однородных структур.
Таким образом, метод условной концентрации является мощным инструментом поиска
границы перехода от режима фрактальной кластеризации к однородности.
Выше мы рассмотрели фрактальные стохастические процессы для частиц одного
сорта. Реальные галактики имеют функцию светимости ![]() , обычно задаваемую
законом Шехтера
, обычно задаваемую
законом Шехтера
описывающим долю галактик со светимостями в интервале
где
Стохастические процессы, в которых фрактальные носители (положения частиц)
характеризуются различными значениями некоторой случайной величины ![]() (например, светимости
(например, светимости ![]() или массы
или массы ![]() ), относятся к классу мультифрактальных
процессов. Рассмотрим реализацию такого стохастического процесса, которая
характеризуется следующей реализованной плотностью светимости (массы):
), относятся к классу мультифрактальных
процессов. Рассмотрим реализацию такого стохастического процесса, которая
характеризуется следующей реализованной плотностью светимости (массы):
В таком случае функция плотности (светимости, массы) галактик является мультифрактальной мерой на множестве реализаций. Мультифракталы характеризуются спектром фрактальных размерностей
Пусть ![]() - число галактик со светимостями в интервале
- число галактик со светимостями в интервале ![]() в сферической
оболочке
в сферической
оболочке ![]() с центром в точке
с центром в точке ![]() , принадлежащей структуре. Обобщая понятие
условной концентрации (5) одинаковых
частиц на случай частиц, характеризующихся разными значениями светимости
(массы), введем условную плотность светимости (массы) галактик в виде
, принадлежащей структуре. Обобщая понятие
условной концентрации (5) одинаковых
частиц на случай частиц, характеризующихся разными значениями светимости
(массы), введем условную плотность светимости (массы) галактик в виде
Можно показать, что для широкого класса мультифрактальных стохастических процессов условную плотность светимости можно представить в виде
При этом шехтеровский вид функции светимости получается как следствие мультифрактальности, а не как дополнительное предположение. Особенностью выражения (12) является зависимость параметра излома функции светимости от радиуса области
4. Методы анализа структуры
На практике при изучении свойств крупномасштабной структуры процедура анализа каталогов оказывается достаточно сложной. Собственно анализу структуры должен предшествовать выбор определенной космологической модели, получение абсолютных величин галактик с учетом K-поправки, поглощения света, эффектов эволюции и пр., учет «геометрических» особенностей каталога (формы области, охваченной каталогом на небесной сфере и краевых эффектов), выделение достаточно полных по светимости выборок галактик, ограниченных по размеру. Только после этого можно приступать к выделению структуры.
Наиболее распространенным подходом к анализу крупномасштабной структуры Вселенной является метод корреляционных функций.
Корреляционная функция определяется как мера вероятности отклонения
распределения частиц от пуассоновского однородного распределения на расстоянии
![]() от
некоторой фиксированной частицы из данной выборки. Для определения двухточечной
корреляционной функции
от
некоторой фиксированной частицы из данной выборки. Для определения двухточечной
корреляционной функции ![]() необходимо рассмотреть две бесконечно малые сферы в
точках
необходимо рассмотреть две бесконечно малые сферы в
точках ![]() и
и ![]() с объемами
с объемами ![]() и
и ![]() , тогда совместная вероятность найти одновременно объекты
в сферах, расстояние между которыми равно
, тогда совместная вероятность найти одновременно объекты
в сферах, расстояние между которыми равно ![]() , будет
, будет
где
Для получения оценки
где
Наиболее существенным предположением, лежащим в основе определения корреляционной функции, является условие априорного существования средней плотности числа объектов, которая не зависит от величины рассматриваемого объема. В частности, это предположение позволяет использовать бесконечно малые объемы в формуле (13).
Если пространственное распределение объектов характеризуется некоторой случайной функцией плотности, то флуктуации этой функции можно представить в виде интеграла Фурье как суперпозицию плоских пространственных волн
где Фурье-образ
Таким образом, полное описание пространственного распределения плотности объектов должно включать рассмотрение как спектра амплитуд
В случае гауссовых случайных процессов фазы плоских волн распределены
равномерно в интервале ![]() и для характеристики поля плотности достаточно
рассматривать только спектр мощности
и для характеристики поля плотности достаточно
рассматривать только спектр мощности
В случае изотропных распределений спектр мощности и корреляционная функция связаны соотношением
Так что для степенной корреляционной функции
Большинство работ, посвященных анализу крупномасштабной структуры, используют
только спектр мощности ![]() , хотя фазовый спектр несет в себе важную дополнительную
информацию о негауссовости процесса кластеризации объектов.
, хотя фазовый спектр несет в себе важную дополнительную
информацию о негауссовости процесса кластеризации объектов.
Для стохастических фрактальных процессов также можно провести Фурье-анализ
функции плотности. Можно ввести понятие масштабно независимого (обобщенного)
спектра мощности фрактальных процессов ![]() , который определяется
выражением, аналогичным (19), где
вместо
, который определяется
выражением, аналогичным (19), где
вместо ![]() под интегралом стоит условная плотность
под интегралом стоит условная плотность ![]() (5), так что
(5), так что
В случае стохастических фрактальных процессов
Топология распределения представляет собой статистику, определяющую так называемый «род поверхности». Данная статистика проводится по сглаженному точечному распределению, которое получается при построении поверхностей одинаковой плотности. При этом исследуемый объем разделяется на области пониженной и повышенной плотности гладкими поверхностями.
Род ![]() поверхности определяется как
поверхности определяется как
| (20) |
где
Для сферы ![]() , для
, для ![]() изолированных сфер
изолированных сфер ![]() , для тора
, для тора ![]() .
Вообще
.
Вообще ![]() равен максимальному количеству принципиально различных разрезов
поверхности, которые можно сделать, сохранив целостность тела.
равен максимальному количеству принципиально различных разрезов
поверхности, которые можно сделать, сохранив целостность тела.
Минимальное охватывающее дерево - один из способов выявления кластеризации объектов. На объектах выборки строится граф (можно показать, что получающийся в результате граф единственен, поэтому начинать построение можно с любого объекта выборки). На некотором шаге происходит поиск объекта, находящегося на наименьшем расстоянии от какого-либо объекта, уже присоединенного к графу. Эти два объекта соединяются ребром. Далее процесс повторяется, пока все объекты выборки не будут присоединены к графу. После построения графа имеются данные о длинах ребер, соединяющих объекты, и о количестве ребер, присоединенных к каждой вершине графа. Используя эти данные, можно выделять объекты, находящиеся в областях повышенной и пониженной плотности.
Перколяция - один из методов кластерного анализа, используется для объединения областей повышенной плотности. Вокруг объекта, выбранного начальным, описывается сфера некоторого радиуса (перколяционный радиус - единственный задаваемый параметр этого метода). Если в сферу попадают объекты, вокруг них тоже описываются сферы того же радиуса, и так далее, пока ни в одну сферу не попадет ни один новый объект. Далее выбираются новые объекты, не вошедшие в кластеры, полученные ранее. Потом можно найти центры масс кластеров и отметить их как новые объекты. Таким образом, например, создавался известный каталог сверхскоплений Эйнасто.
Существуют также как многочисленные модификации перечисленных методов, так и менее распространенные статистики, используемые для изучения распределения астрофизических объектов. Например, более детальное построение трехмерной картины ближайших областей Вселенной послужило толчком к развитию разнообразных статистических методов выделения и исследования различных структур в распределении объектов во Вселенной - «пустот» (voids), «цепочек» (filaments), сверхскоплений («стен», состоящих из галактик). В отличие, например, от двухточечной корреляционной функции эти методы более тонко выделяют морфологические особенности структур.
5. Современное состояние
Несмотря на то, что распределение видимого вещества в сравнительно малых масштабах очевидно неоднородно, наиболее распространено мнение, что существует верхняя масштабная граница неоднородности. В то же время среди исследователей нет согласия в вопросе о том, на каких масштабах наблюдаемая неоднородность заканчивается.
Задача усложняется тем, что выборки, используемые для анализа структуры, как
правило, недостаточно хороши в области больших масштабов, поэтому исследователи
крупномасштабной структуры уже неоднократно сталкивались с ситуацией, когда
неоднородность на каком-то масштабе по данным обработки некоторого каталога
предположительно заканчивается, но позднейшая обработка более полного и
глубокого каталога показывает, что это впечатление было обманчивым. На данный
момент оценка пограничного масштаба колеблется у разных авторов от ![]() до
до ![]() Мпк.
Мпк.
Неясен также и статус фрактальных моделей крупномасштабной структуры.
Диапазон мнений, существующих по этому поводу, крайне широк - от
абсолютизации фрактальной модели до полного ее неприятия. Однако большинство
специалистов склоняется к мнению, что на масштабах до ![]() Мпк
крупномасштабная структура по меньшей мере хорошо описывается фрактальным
распределением с фрактальной размерностью
Мпк
крупномасштабная структура по меньшей мере хорошо описывается фрактальным
распределением с фрактальной размерностью ![]() . Для описания
структуры на больших масштабах простейшая модель самоподобного фрактала,
по-видимому, непригодна.
. Для описания
структуры на больших масштабах простейшая модель самоподобного фрактала,
по-видимому, непригодна.
Из несостоятельности модели самоподобного фрактала не следует невозможность более сложной, мультифрактальной модели фрактальной структуры. В этом случае физическая система обладает локальным свойством самоподобия, но масштабные свойства определяются спектром фрактальных размерностей. В рамках такой модели существующие данные о крупномасштабной структуре описываются достаточно хорошо.
В настоящее время объем наблюдательных данных о крупномасштабной структуре быстро увеличивается. Однако многие результаты, полученные в этой области астрофизики, а иногда и использованные при этом методы остаются спорными. Наведение «порядка» в представлениях о крупномасштабной структуре, по-видимому, является делом будущего, хотя и ближайшего.
Литература
- 1. Барышев Ю. В. Пространственное
распределение галактик и тесты релятивистской космологии: Дисс. д-ра физ.-мат.
наук. СПб., 2003.
- 2. Пиблс Ф. Дж. Э. Структура Вселенной в больших масштабах. М.: Мир. 1983.
- 3. Тараканов П. А. Фрактальные структуры и неравновесные системы в астрофизике // Физика космоса: Тр 33-й международ. студ. науч. конф., 3-7 февр. 2003 г. Екатеринбург: Изд-во Урал. ун-та, 2003.
- 4. Тихонов Н. А. Распределение галактик и систем галактик в наблюдаемой Вселенной: Дисс. канд. физ.-мат. наук. СПб., 2002.
- 5. Guzzo L. Large-scale structure from galaxy and cluster surveys. astro-ph/0207285. 2002.
- 6. Martinez V. J., Saar E. Statistics of the galaxy distribution. Chapman&Hall/CRC. N.Y., 2002.
- 7. Sylos Labini F., Montuori M., Pietronero L. Scale-invariance of galaxy distribution // Phys. Rep. 1998. Vol. 293. P. 61.
- 8. Sylos Labini F., Gabrielli A., Pietronero L. Statistical Physics for Cosmic Structures. Springer-Verlag, 2003.
- 2. Пиблс Ф. Дж. Э. Структура Вселенной в больших масштабах. М.: Мир. 1983.
| Публикации с ключевыми
словами: крупномасштабная
структура Вселенной Публикации со словами: крупномасштабная структура Вселенной |
|
См. также:
Все публикации на ту же тему >> | |