Каминский А.В.
Возможно ли алгоритмическое описание мира?
Тот же, кто подходит к философии, как математик, требуя дефиниций и дедукций
в математическом стиле, поступает ничуть не умнее зоолога, который стал бы
отвергать числа на том основании, что они не являются живыми существами.
| |
|
Г.Вейль, "Континуум"
|
Вычисления и физика.
Успехи теории квантовых вычислений, достигнутые в последние годы, значительно опередили возможности современной технологии и потому едва ли могут оказаться практически полезными в ближайшие годы. Однако, они вплотную подвели нас к еще не тронутому кладезю предоставляемых природой квантовых ресурсов, освоение которых ознаменует небывалый прорыв в области информационных технологий. Исследования Р.Фейнмана, П.Бенеффа, Р.Ландауэра, Д.Дойча, П.Шора, Е.Фредкина, Т.Тоффоли и других первопроходцев в этой области внесли незаменимый вклад в изучение самых фундаментальных и интригующих вопросов мироустройства, приблизили нас к пониманию сущности времени, квантовой природы мира и ряда других фундаментальных вопросов. Переосмыслен ключевой принцип, на котором основывается вся теория вычислений - тезис Черча-Тьюринга.
Более 60 лет мы были убеждены в том, что вычислимы только те функции, которые могут быть вычислены машиной Тьюринга. Это, так называемый, класс частично-рекурсивных функций. Тезис Черча-Тьюринга придает этому классу универсальный статус, утверждая, что любой возможный в нашем мире вычислительный процесс эквивалентен машине Тьюринга (МТ), и потому любая вычисляемая нами функция принадлежит этому классу. Тьюринг даже не подозревал, что это утверждение содержит неявное физическое предположение. Дойч пишет: "Несмотря на то, что истины логики и чистой математики объективны и не зависят от случайных обстоятельств или законов природы, наше знание этих истин полностью зависит от законов физики. Последние достижения в теории квантовых вычислений на примерах подтвердили этот факт. И это заставляет нас отбросить традиционный взгляд на то что математические истины и чистые логические понятия не зависят от вычисления, как физического процесса". Еще не так давно мы были готовы поверить в первичность математических идей. В русле такого понимания лежит и концепция геометризации физики, которая провозгласила, что в мире нет ничего, кроме пустого искривленного пространства. Стремясь же быть до конца последовательными, мы даже готовы были согласиться с тем, что весь наш "грешный" мир - большая машина Тьюринга. И тогда все вокруг и мы с вами - со всеми нашими мыслями и чувствами описывались бы набором поистине простых рекурсивных функций. В научной литературе эта тема обсуждалась довольно широко. Аналогичную возможность исследовал и автор в работе "Алгоритмическая модель мира". Однако, следуя законам диалектического развития, наша мысль уже в который раз возвращается к пониманию подчиненности математических идей трансцендентной физической реальности. И тем не менее вопрос остается. В настоящей работе мы обсудим правомерность этих подходов. В статье [1] Дойч предлагает модифицировать тезис Черча-Тьюринга следующим образом: "Каждая конечно реализуемая физическая система может быть полностью промоделирована универсальной моделирующей вычислительной машиной, действующей конечными средствами". В этой же работе Дойч строит модель такого универсального компьютера, основанную на идее квантовых вычислений. В чем же состоит открытие Дойча? Во первых, он предложил расширить класс вычислимых функций, объявив вычислимыми те функции, которые могут быть вычислены реальной физической системой, то есть функции вычисляемые самой природой. Во вторых, он заменил МТ на универсальный квантовый компьютер, в дальнейшем MQ. Идея понятна, - трудно считать функции невычислимыми, если они вычисляются природой и наоборот. Обычно считается, что функции, вычисляемые природой, всюду плотны на континууме, тогда как функции, вычисляемые моделью Тьюринга, составляют лишь перечислимое множество всех функций из Z в Z. Поэтому и возникла идея "офизичивания" тезиса Черча-Тьюринга. Несмотря на то, что никому еще не удалось показать, что класс функций, вычисляемых природой шире класса частично-рекурсивных функций и все рассуждения, касающиеся этого вопроса носят чисто эмпирический характер, есть серьезные основания думать именно так.
В работе [2] в главе "2.3 Бесконечность в модели конечного мира" мы показали, что если рассмотреть конечную модель мира, то для субъекта этого мира сам мир будет бесконечным, и никакие финитные методы, которыми он, субъект располагает не могут быть достаточны для адекватного моделирования им его "физической реальности". Однако, возможно асимптотическое приближение к функциям "вычисляемым" природой по мере усложнения модели. Мы еще вернемся к этому важному вопросу ниже, когда будем рассматривать подобную модель.
В литературе по квантовым вычислениям часто можно встретить утверждение, что MQ способен моделировать некоторые процессы в принципе не поддающиеся моделированию классическими средствами. К таким процессам, в частности, относят квантовые корреляции. Это утверждение находится в явном противоречии с нашим представлением о сущности моделирования. К обсуждению этого вопроса мы сейчас и приступаем.
Моделирование и реальность.
Прежде всего давайте разберемся, в чем сущность моделирования и в чем заключается цель вычисления. Человек проще мира, в котором он живет, ибо является его частью. Поэтому его знания о мире не могут быть полны в принципе. Здесь имеется глубокая аналогия с неполнотой непротиворечивых аксиоматических систем, исследуемых математической логикой. Следует ясно понимать, что эта неполнота не является временным или второстепенным явлением, но лежит в самой основе физической реальности, понимаемой в контексте субъект-объектных отношений, имеющих место в самодостаточном замкнутом мире. Одним из следствий физической неполноты является следующее: Средствами части Мира, каковой и является субъект, невозможно с тождественной точностью смоделировать процессы, для описания которых требуются большие вычислительные ресурсы (объем памяти, время и точность). Однако, всегда возможно приближенное описание, дающее целый ансамбль состояний мира. Именно это является ответом на сакраментальный вопрос - почему в природе должна иметь место квантовая механика. Квантовая механика, как и другие создаваемые нами теории, является моделью реальности и ее неполнота есть характерное свойство любой модели. В этом контексте странным и нелепым кажется наше стремление отождествлять создаваемые модели с реальностью. Копенгагенская интерпретация квантовой механики следует именно такой логике. Однако квантовая механика занимает особое место в ряду моделей, созданных человеком за всю историю естествознания. Волновая функция объекта - наисложнейшая, предельная из всех сконструированных нами моделей. Ниже мы покажем, что могут существовать принципиальные ограничения на точность моделирования. Похоже, что в случае квантовой механики мы уже достигли этого предела. Сущность модели состоит в том, что она проще объекта моделирования. В таком понимании кажется странным введенное Дойчем в вышеупомянутой статье понятие полного моделирования -perfect simulation-. Обычно цели моделирования заключаются в прогнозировании и изучении поведения реальных физических систем с тем чтобы затем учесть их в реальной жизни. Заметим, что возможности экспериментирования с реальными объектами всегда ограничены. Именно, благодаря упрощенному описанию объекта, экспериментатор может изменять значения параметров и начальных условий, масштабировать и изменять направление времени. Как будет меняться алгоритм, интерпретирующий объект, при увеличении точности моделирования? Ясно, что сложность и время его выполнения будут расти. Кроме того, модель все более будет походить на объект моделирования, а у исследователя будет оставаться все меньше возможностей для экспериментирования. Экстраполируя эту тенденцию, легко понять, что модель при увеличении точности, приближается к самому объекту моделирования. А.Н. Колмогоров писал: "Достаточно полная модель живого существа по справедливости должна называться живым существом, модель мыслящего существа- мыслящим существом". Ключевым словом в этом высказывании является слово "достаточно". Может быть, достаточно полная модель - это копия? Фон Нейман, размышляя над механизмом человеческого мышления, пришел к гипотезе, что, если система достигает определенной степени сложности, то ее модель не может быть проще, чем она сама. Этот тезис аналогичен только что приведенному высказыванию Колмогорова.
Так что же означает полное моделирование по Дойчу? Он пишет: "Вычислительная машина M может полностью промоделировать физическую систему Y относительно данной разметки их входов и выходов, если для M существует программа, которая делает M вычислительно эквивалентной Y относительно этой разметки." Это определение имеет смысл до тех пор, пока речь не идет о максимально сложных физических объектах [2], которые не допускают упрощения. Полное моделирование таких объектов есть не что иное, как копирование. Однако, не говоря даже о том, что клонирование квантовых состояний запрещено [3], такое "моделирование" было бы лишено смысла. По-видимому, имея в виду именно это ограничение, Дойч указывает, что MQ не может быть использован для вычисления мировых констант.
Мы нисколько не принижаем значения открытия квантовых вычислений, но пытаемся найти место квантового компьютера в базе таких понятий, как моделирование, вычисление, вычислимость и физическая реальность. Будучи создан, MQ несомненно будет практически полезен, ибо позволит решать задачи из класса "NP" (Задачи не решаемые классическим компьютером за полиномиальное время). Примером тому является алгоритм факторизации больших чисел, найденный Шором [4]. Однако, скажем, для моделирования квантовых эффектов, он не более полезен, чем МТ. Эта особенность обусловлена его предельностью. Дело в том, что Q-биты [5] являются элементарными сущностями физической реальности. Можно ли взяв за основу теории, скажем, кофемолку построить модель работы той же кофемолки? Очевидно нет. Точно так же, взяв за основу моделирования квантовое состояние, мы никогда не проникнем в его сущность. Однако, того кто "исповедует" Копенгагенскую интерпретацию это вполне устраивает. Если речь идет о моделировании квантовых свойств материи (не путать с моделированием квантовых систем !), то в этом случае MQ не может выполнять моделирующие функции, и является как бы "генератором" полнофункциональных физических объектов. Действительно, программа MQ может поставить любой физический эксперимент. Но это будет реальный физический эксперимент - копия той ситуации, которая может быть реализована в природе, а не модель процесса. И все возможности и преимущества, даваемые моделированием не будут реализованы. Поэтому, мы не можем согласиться с Фейнманом [6] и Дойчем, утверждающими, что классический компьютер не может моделировать квантовую реальность. Более того, почти очевидно, что эффективность квантового и классического компьютера в этом случае будут близки.
Рассмотрим в качестве примера, каким образом на классическом компьютере могут быть смоделированы квантовые корреляции ЭПР-типа [7].
Сущность явления состоит в следующем. Пусть, мы проводим измерение над квантовой системой, состоящей из двух разнесенных в пространстве частей, так, что события измерения разделены пространственно-подобным интервалом. И пусть изначально система приготовлена в состоянии суперпозиции чистых состояний ψ1 и ψ2. Пусть, далее, для измерения над первой частью мы применяем либо прибор "A1", либо прибор "A2", а над второй либо "B1", либо "B2". Собственные значения операторов "A1,A2,B1,B2" дают измеряемые этими приборами величины "a1,a2,b1,b2".
Достаточно произвести измерение только над одной из частей системы, чтобы другая часть немедленно зафиксировала свое состояние, невзирая на то, что эти части могут быть причинно не связаны. Но важен не сам факт корреляции, которая может выражать закон сохранения энергии или углового момента, но факт более сильной корреляции, не объяснимой классической физикой. Критерий отличия классических корреляций от квантовых был найден Беллом и выражается в виде неравенства: |<ab>-<a1b>+<ab1>+<a1b1>| ≤ 2. Угловыми скобками здесь обозначены корреляционные функции соответствующих наблюдаемых. Ключевой эксперимент Аспекта по двухфотонной корреляции показал, что передача информации осуществляется именно в момент коллапса волновой функции и, следовательно, никакой априорной информации части системы не несут. Получается, что первая часть системы как-то передает второй части информацию о том проводилось ли над ней измерение и какой оно дало результат именно в момент коллапса, нарушая все наши представления о локальности и причинности.
Рассмотрим, для простоты обычную схему эксперимента по корреляции фотонов. Пусть в результате двухфотонного перехода источник света излучает 2 фотона, разлетающихся в противоположных направлениях к приборам "A", и "B" соответственно. Закон сохранения четности гарантирует, что если первый фотон X-поляризован, то другой тоже X-поляризован. Угол же поляризации Ф, относительно условно выбранного направления случаен. Пусть первый и второй наблюдатели применяют приборы "A1" и "B1" соответственно, ориентированные под углом Ф1. Вероятность того, что первый наблюдатель (прибор "A1") обнаружит X-поляризацию равна:
P1x=1/2Cos2(Ф-Ф1)
Вероятность, что при этом второй наблюдатель, применив прибор "B2", ориентированный под углом Ф2, обнаружит X-поляризацию равна
P2x=1/2Cos2(Ф1-Ф2)
Можно написать простейшую программу, имитирующую такое поведение.
В псевдокоде программа может иметь вид:
Procedure MESSURE(Ф,Ф0)
Begin
If Random(1)>Cos2(Ф-Ф0) then Ф=Ф0
Else Ф=Ф0+90˚
End.
----------------------------------------------
Main Program
Begin
Read (Ф1,Ф2)
Ф=Random(360˚)
Call MESSURE(Ф,Ф1)
Print Ф
Call MESSURE(Ф,Ф2)
Print Ф
End.
----------------------------------------------
Здесь вначале описана процедура измерения MESSURE(), Передача параметров осуществляется через переменную Ф в обоих направлениях. Процедура управляет функцией распределения вероятности обнаружения той или иной поляризации. В теле процедуры использован генератор псевдослучайных чисел. Основная программа является протоколом проведения эксперимента. В начале экспериментатор задает углы Ф1 и Ф2 ориентации применяемых приборов "A", и "B". Далее источник света испускает фотоны со случайной (0-360˚) поляризацией Ф. Затем один за другим производят измерения оба наблюдателя. Значения углов полученных поляризаций выводятся на печать. Легко убедиться, что программа, действительно, описывает квантовые корреляции и как и следовало ожидать нарушает неравенства Бэлла. Каким же образом программа имитирует квантовую нелокальность? Секрет очень прост. Все дело в том, что результат измерения Ф, полученный первым наблюдателем "нелокально" передается в процедуру измерения второго наблюдателя. Такой подход к интерпретации квантовой механики известен, как теории скрытых переменных. Обычно считается, что нарушение неравенства Белла доказывает невозможность описания реальности посредством локальных скрытых переменных. И если бы удалось "изобрести" нелокальный способ передачи параметров, - квантовая механика была бы обоснована.
- Но то, что вы сделали - это обман, скажете вы!
- Вы не моделируете нелокальность, а "подсовываете" ее нам в готовом виде.
Однако, не торопитесь с выводами. Действительно все, что мы пока сделали -
это даже не модель, а некая наивная аналогия. Нелокальность в ней возникает
благодаря тому, что мы просто отказываемся рассматривать сам механизм передачи
параметра Ф.
Давайте подумаем о том, какой будет физическая реальность для наблюдателя, который даже не догадывается о том, что в его мире может иметь место некий механизм реализующий нелокальность. Более того, пусть эта физическая реальность такова, что любая попытка обнаружить этот механизм будет безуспешной. Очевидно, что наш наблюдатель вынужден будет "изобрести" свою Копенгагенскую интерпретацию.
Но, что за причина может помешать нам обнаружить этот самый скрытый механизм? Очевидно, эта причина должна быть весьма принципиального характера. Продолжим рассмотрение нашей компьютерной аналогии. Пользователю, как правило, доступна только внешняя сторона работы программы, тогда как процессы, осуществляемые на более глубоком уровне иерархии программного обеспечения скрыты от него. Однако, нам необходимо как-то онтологизировать это невосприятие субъектом-наблюдателем "тонких" процессов происходящих в компьютере. (В противном случае, обнаружив эти процессы, наш наблюдатель "доберется" и до механизма передачи параметра "Ф" и констатирует его локальный характер). Этого легко можно добиться, если допустить, что для нашего наблюдателя минимальным временным интервалом, или квантом времени, является один шаг приведенной выше программы, тогда как вся необычайно сложная динамика работы компьютера, характеризующаяся значительно меньшими характерными временами, останется скрытой от него вследствие невосприятия им столь малых временных интервалов. Конечно проще всего было бы постулировать наличие кванта времени. Например, взяв за основу Планковское время ∀10-43 сек. Однако, в модели субъект-объектного мира, которую мы рассматриваем ниже, в таком искусственном приёме не возникает необходимости, ибо возможности восприятия субъектом реальности в ней ограничиваются естественным образом.
Так или иначе, важно понимать, что человек всегда имеет дело с моделями объектов и никогда с истинными объектами. Причем степень детализации этих моделей зависит от глубины нашего знания, принципиально ограниченной сверху. Этим мы с одной стороны обосновываем трансцендентность истинной реальности, существование которой предполагаем в метафизическом плане, а с другой онтологизируем понятие модели мира как физической реальности.
Проблема интерпретатора.
Казалось бы, столько сказано и написано на эту тему, что добавить нечего. Однако, мы хотели бы заострить внимание читателя на одном важном моменте, который хотя и упоминается при описании МТ, но не удостаивается должного внимания. Это проблема интерпретатора или процессора. Как известно, МТ представляет собой ленту с данными (память данных) и таблицу с предписанием того, что делать с этими данными (память программ). Но сразу же возникает вопрос. Кому или чему адресовано это предписание? Иногда можно услышать о механизме, передвигающем ленту, печатающей головке и т.д. Но эти рассуждения всегда неконкретны и создается ощущение, что эти вопросы не принципиальны. В действительности речь касается устройства, которое в вычислительной технике называют процессором, способного распознавать символы на ленте (в памяти данных) и в соответствии с тем как они соотносятся с другой информацией, хранящейся в таблице состояний МТ (в памяти программ) менять информацию в памяти данных. Таким образом, процессор по сути является интерпретатором. Программа МТ имеет смысл только по отношению к соответствующему интерпретатору.
Роль процессора может выполнять либо человек с карандашом и листом бумаги, либо другая МТ, интерпретирующая работу первой МТ и, заметьте, в свою очередь требующая интерпретации. В конечном счете мы приходим к необходимости базового звена интерпретации, которая осуществлялась бы посредством некоего аппаратного обеспечения - HardWare, будь то человеческий мозг или логическая цепь. Но если подумать глубже, то спуск по этой иерархии не ограничивается. Дело в том, что сам HardWare требует интерпретации. И этим интерпретатором является материя, управляемая физическими законами. Но что является интерпретатором самой физической материи? Более "тонкая материя"? Похоже, что не существует того главного, первичного интерпретатора, находящегося в вершине рассматриваемой иерархии, и тогда имеет место бесконечный регресс. В связи со сказанным, возникают очевидные трудности при попытке использовать МТ в качестве модели мира. Действительно, требования замкнутости и самодостаточности, обычно предъявляемые к моделям мира, находятся в явном противоречии с необходимостью внешней интерпретации и, следовательно, приводят к невозможности замкнуть модель. Мы не отказываемся от очевидного факта наличия такой вложенной структуры, но мы не можем признать, что она бесконечна. Наше представление о бесконечности, как относительном субъективном понятии, противится такому пониманию.
Однако, противоречия удается избежать, если отказаться от понятия алгоритма как абсолютного априорного понятия. Этим мы и воспользуемся в следующей главе предпринимая честолюбивую попытку построить самодостаточную модель мира.
Построение мира.
Будем исходить из следующих посылок:
- Мир самодостаточен.
- Мир конечен.
- В основе мира лежит неупорядоченное множество N фундаментальных сущностей. {A1,A2,-,AN}
Требование самодостаточности подразумевает естественное желание построить модель мира, в которой свойства объектов и отношения между ними определялись бы посредством самого мира и не требовали внешнего наблюдателя.
Конечность мира не столь тривиальное требование и потому необходимо более пространное разъяснение. Традиционно счетная бесконечность определяется потенциально, как незавершаемый итерационный процесс прибавления единицы. В этом смысле бесконечность не число, а процесс. Актуализируя бесконечность, то есть объявив ее числом, Кантор сделал первый шаг к "офизичиванию" бесконечности. Подобно тому, как Дойч модернизировал понятие вычислимости, поставив его в зависимость от физического мира, мы введем понятие физической бесконечности.
Разумно конечным числом считать такое число, которое субъект этого мира способен прочитать и понять. Предположим субъект, в виду своей конечности, может оперировать числами не более чем 2n, где N длина двоичной записи числа. Такое ограничение может иметь место если память субъекта физически не способна отразить число большей разрядности. Можно подумать, что это ограничение не столь фундаментально. Ведь субъект всегда может позаимствовать запоминающие ячейки из внешней среды, и в случае необходимости обработать числа большие, чем 2N.
Представим себе, однако, тот крайний случай, когда субъект "позаимствовал" половину всех мировых "вычислительных ресурсов" (Здесь мы предполагаем, что модель мира конечна). Тогда, если весь мир представим двоичным словом длины N, то числа большие 2N/2 с точки зрения субъекта следует считать бесконечными. Так как реально эти числа конечны, мы их назовем субъективно или физически бесконечными. Из этого простейшего анализа мы видим, что нет необходимости считать мир бесконечным. Понятие бесконечного возникает как свойство субъект-объектного отношения в конечном мире.
Для того, чтобы не допустить порочного логического круга или смысловой рекурсии мы не будем привносить в конструируемый мир сущности извне и используем внешний или мета-мир исключительно как вспомогательное средство в нашем построении. Точно так же, как выход в гиперпространства помогает осмыслению сложных геометрических образов. Этому должен способствовать наш метод.
Алгоритм, рассматриваемый как "черный ящик", является функцией биективно отображающей множество, называемое областью данных на себя. Такая функция, будучи задана таблично, представляет собой множество субъектно-упорядоченных пар. Понятие же упорядоченности, не содержится в симметричной аксиоматике математической логики, и как родовой, категориальный элемент, необходимый для всех математических построений, привносится туда всякий раз искусственно, оставаясь неформализован. Другими словами, смысл любого математического построения, в конечном счете, оказывается замкнут на сознании математика. Попытки же замкнуть теорию на себя, как известно, приводят к множеству трудно устранимых парадоксов, среди которых и известный парадокс Б.Рассела. Лишение же экзистенциального статуса унарных отношений (самоприменимость математических понятий), как это делает аксиоматическая теория множеств создает серьезные барьеры для проникновения математики в сущность рефлексии и сознания. С аналогичными трудностями встречается любая попытка построения алгоритмической модели мира.
Не существует внешнего, по отношению к миру, наблюдателя, способного замкнуть на себе смысл упорядоченности и сформировать представление об алгоритмичности мира. Мы допускаем грубую методологическую ошибку, пытаясь объект, по сути являющийся компонентом субъект-объектной целостности, превратить в замкнутую самосогласованную структуру. Объект всегда будет открыт для субъекта. Единственный выход - формализовать понятие субъекта, сделав его частью модельного мира. То есть построить метатеорию субъект-объектного мира. Но сделать это осторожно, чтобы после того, как теория будет построена, аккуратно обрезать нити новых гиперсубъектных отношений. Это можно будет сделать, отождествив внешнего наблюдателя с субъектом модельного мира.
Рассмотрим что есть упорядоченное множество и по отношению к чему устанавливается смысл упорядоченности? Очевидно, что только по отношению к внешнему мета-наблюдателю. Но мы не можем считать мир априорно упорядоченным ибо это заставило бы нас отвечать на вопрос, почему в мире реализуется именно этот упорядочивающий принцип, а не другой. Водном из писем Морису Cоловину Эйнштейн писал: "Ну что же, априори, следует ожидать хаотического мира, который невозможно познать с помощью мышления. Можно (или должно) было бы лишь ожидать, что этот мир лишь в той мере подчинен закону, в какой мы можем упорядочить его своим разумом...". Обычно считается, что множество упорядочено, если возможно установить взаимно-однозначное соответствие его элементов с элементами натурального ряда {N}. Но по отношению к чему упорядочено само множество {N}? Как известно, упорядоченность натурального ряда не может быть задана логически и определяется только по отношению к нашему субъективному пониманию времени и операции "следования за". Таким образом, смысл упорядоченности, в конечном счете, замыкается внутри субъективности внешнего наблюдателя. Как же устранить внешнего наблюдателя из теории?
Для этого эксплицируем смысл неупорядоченности, возникающий у субъекта в отношении к неупорядоченному мировому множеству (первозданный хаос). Будучи негативно-определенным, это понятие потенциально содержит в себе обратный ему смысл упорядоченности. Например понятие "бесцветный" может обозначать "белый". Но белый, как известно, представляет собой смесь всех цветов. Подобно этому, развертывая смысл неупорядоченности, мы получаем ансамбль всех возможных упорядоченностей. Описанный прием порождения объектов, который можно было бы назвать смысловой инфляцией, примененный к неупорядоченному множеству, приводит к целому ансамблю линейно-упорядоченных мировых экземпляров.
Теперь осуществим вскрытие того же смысла уже изнутри нашего неупорядоченного мира. Если мир в целом изначально симметричен, а это вполне естественно предположить, ибо любой асимметрии должна быть причина, то субъекту этот мир будет казаться асимметричным. Дело в том, что в силу неполноты, связанной с принципиально ограниченными возможностями субъекта, ему, субъекту не доступна полная группа симметрий мира (она доступна только внешнему наблюдателю). Поэтому, субъекту мир всегда представляется частично несимметричным. Такое субъективное нарушение симметрии приводит к возникновению в системе относительных смыслов, и прежде всего, экзистенциального смысла бытия самого "Я" в структуре субъект-объектного отношения. Я всегда обнаруживаю себя в одном из неполностью симметричных и соответственно упорядоченных экземпляров мира.
Подобно тому, как совокупность несимметричных секторов, образует симметричную фигуру - круг, мир в целом представляет собой ансамбль всех несимметричных экземпляров и потому симметричен. Таким образом порядок, который я наблюдаю как физическую реальность в действительности является экземпляром хаоса, выделенного в результате трансцендентальной редукции сознания [2]. Несимметричность мирового экземпляра, позволяет нам пронумеровать места вхождения аргументов в бинарных функциях отношений, на основе которых строится математический итерационный процесс [8] и построить алгоритмическую модель.
До настоящего момента мы оставляли в стороне вопрос о категориальном отнесении сущностей, являющихся элементами рассматриваемого неупорядоченного множества. Будем считать, что сущности о которых идет речь изображают состояния нашего мира. Правда такое отнесение имеет смысл только в отношении к внешнему мета-миру. Поэтому, опять посмотрим, на нашу конструкцию со стороны.
Наш мир W по определению неоднороден, так как он конструктивен. Поэтому, всегда возможно условно разделить его на части. Субъектом S назовем условно выделенную часть мира. Объектом будем считать дополнительную к нему часть W\S. Пусть Si некоторое состояние субъекта а Oi состояние объекта. Тогда состояние мира есть пара Ai={Si,Oi}. Внешний наблюдатель может представить состояние мира в виде слова длиной log2N в двухбуквенном алфавите, где N число состояний мира.
Рассмотрим в качестве примера 6-ти битный или 64 сущностный мир. И пусть субъект представлен 4 состояниями (2 бита на рис.1). Так как состояния по определению не связаны, число состояний мира, очевидно, определится как Nwor=Nsub*Nobj, где Nsub - число состояний субъекта, а Nobj - число состояний объекта. Длина мирового слова, соответственно, определится как сумма длин слов субъекта и объекта. (т.к. длина=log2N)
Какие выводы можно сделать из такого элементарного рассмотрения? Субъект, находясь с остальной частью мира в информационном отношении (а только такой тип отношений возможен в рассм. модели), занимает часть "ячеек" или разрядов мирового слова, уменьшая тем самым число состояний оставшейся части мира. Итак, представим себе, что субъект состоит из 2-х ячеек, а остальная часть мира, соответственно, из 4-х.
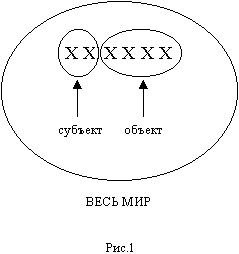
Если считать, что младшие разряды мировых состояний описывают, скрытые состояния, то для восприятия субъектом эти структуры недоступны. Это очевидно, если учесть, что состояний "памяти" субъекта явно недостаточно для того что бы отобразить все состояния объекта. Между состояниями "памяти" субъекта и состояниями объекта перманентно имеют место отношения, которые являются аналогом рефлексии.
В результате субъекту мир представляется относительно упорядоченным множеством "грубых" состояний, представляющих собой некоторые состояния, получаемые комбинированием мировых состояний в группы. Будем называть эти состояния физическими. Обратим внимание на то, что понятие упорядоченности теперь замыкается внутри конструируемого мира, а не в сознании внешнего наблюдателя, как это имело место выше. Принцип упорядочения, определяемый рефлексивным отображением, не привносится извне, но существует, как экземпляр ансамбля всех возможных относительных упорядоченностей.
Таким образом, теперь субъект может определить функцию упорядочения физических состояний и описывать динамику мира алгоритмически. Здесь понятие алгоритма имеет смысл только по отношению к субъекту.
Распишем все состояния мира рис.2.
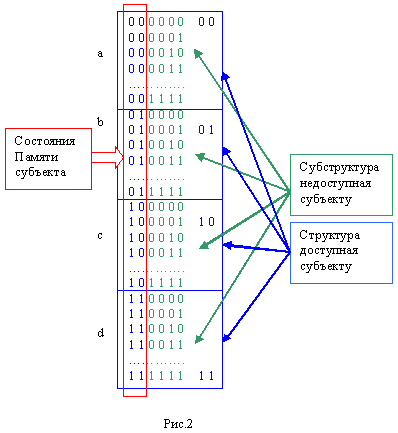
На рисунке приведен один из 4!=24 экземпляров мира, когда субъект установил определенное отношение между состояниями памяти и различаемыми им вырожденными физическими состояниями "a","b","c","d". Установление такого отношения есть построение модели реальности. Мировые состояния конфигурационны. То есть это состояния типа Субъект-в-мире. Субъект в нашем примере способен различить 4 физических состояния. Каждый такой объект, как видно из рисунка, имеет внутреннюю тонкую структуру из 16 мировых состояний, скрытую от субъекта. Субъект в нашем 6-ти битном мире может заимствовать из мировых ресурсов от 1 до 6 бит. В зависимости от этого наблюдаемая им "физическая" реальность будет различаться.
Все состояния мира существуют актуально и вневременно. И состояние в котором субъект столь примитивен, что имея только два состояния памяти во всем мировом многообразии различает только две сущности. Этот случай можно отнести к эпохе "зарождения мира", когда "Бог" отделил свет от тьмы и 0 от 1. И промежуточное состояние, когда субъект занимает половину всех мировых состояний, так, что другая их половина биективно рефлектируется субъектом. Такая ситуация может реализоваться в будущем и соответствует пределу познания внешнего мира. А также крайняя ситуация, когда субъект поглотил все ресурсы мира. Возможно, эту ситуацию следует интерпретировать, как полное познание субъектом своей субъективности.
Но оставим возможность интерпретации фантастам и рассмотрим что дает наша модель. Прежде всего- это наличие в модели нелокальных скрытых переменных. И это позволяет довольно естественным образом подступиться к проблеме обоснования квантовой теории, объяснить ряд вопросов из области статистической механики, и в частности обосновать закон возрастания энтропии [9]. Модель органически включает сознание субъекта в структуру мира.
Многослойная реальность.
Общая тенденция к поиску самосогласованной структуры мира привела в последнее время к тому, что процесс познания невозможно уже рассматривать вне онтологического контекста.
В этом же русле лежит и предложенная Дойчем увязка понятия вычислимости с физикой. Вычислимость по Дойчу - это вычислимость реальным физическим компьютером (не тем, что у нас на столе, но любым возможным в этом мире. В терминологии мировых слоев можно сказать, что Дойч говорит о вычислимости в нашем реальном физическом слое, тогда, как Тьюринг - о вычислимости в условном виртуальном мире, описываемом системой аксиом, урезанной до аксиоматики Пеано. Но слой Тьюринга реально существует. Это слой нашей ментальности, мир нашего рационального мышления, в отличие от слоя квантовой реальности, или следующего в иерархии, слоя нашей субъективности, в котором такие понятия, как число и натуральный ряд даны нам исключительно в форме априорного знания.
В примере, рассмотренном выше, явно выделяются 2 слоя реальности. Первый слой, доступный только внешнему гипотетическому наблюдателю, который можно назвать слоем высшей реальности или "тонким миром". В нашем примере этот слой состоит из 64 состояний. И второй - слой субъекта. Этот слой уже не столь многообразен и имеет всего 4 состояния. Этот слой можно назвать физической реальностью, так как физическая реальность - это то, как мир видится субъекту. Таким образом, физическая реальность в нашей интерпретации относительна и непостоянна. Она определяется степенью нашего знания. В связи с этим создается ощущение, что рассматриваемая проблема имеет гносеологический характер. Но наше представление о мире вынуждает нас онтологизировать это понятие. Так же как наше знание о состоянии квантового объекта определяет физику его поведения, точно так же наше знание о мире определяет, подчеркиваю не в психологическом или гносеологическом плане, а физически, ту реальность, в которой мы живем. Опередим читателя, уже готовящегося обвинить нас в одной из крайних форм субъективного идеализма, и очертим нашу позицию в этом вопросе. Во первых, мы считаем, что мир существует объективно и только физическая реальность субъективна. Во-вторых, субъективность мы отделяем от индивида и, онтологизируя это понятие, лишаем его психологической окраски. Если уж говорить о ярлыках, то нашу концепцию скорее можно было бы назвать субъективным материализмом, чем идеализмом.
Почему мы онтологизируем многослойность физической реальности? Дело в том, что нам ясно видится связь знания с реальностью. Мы что-то знаем о мире, а что-то можем узнать еще. Здесь, казалось бы, чистая гносеология. Но вот перед нами непознанный объект. Электрон, структура которого нам неизвестна, или сам Мир в целом, включающий самого наблюдателя. И здесь проблема уже становится онтологической. Структуры или объекты, недоступные нашему анализу в силу каких-либо физических причин, скажем, недостатка вычислительных ресурсов для моделирования, имеют статус трансцендентных, ведь мы не можем структурировать их отношение с субъектом. Такими объектами в приведенном выше примере являются группы "a","b","c","d". Множество таких объектов представляет собой базовый набор простейших элементов физической реальности, из которых субъект в своем сознании строит картину своего физического мира (слоя). С этой точки зрения, очевидно, что объективная реальность нашего мира в действительности принципиально субъективна, ибо это единственная данная нам реальность. Мы никогда не возвысимся до Бога, чтобы увидеть мир со стороны и постигнуть реальность вышележащего слоя в структуре мировой иерархии. Мы, конечно, можем построить модель этой реальности. Но модель и объект моделирования всегда лежат в разных слоях. Пока что мы говорим о двух слоях мира - слое нашей физической реальности и вышележащем слое, в котором скрыты истинные смыслы наблюдаемых нами феноменов. Похоже, что квантовая механика лежит как раз на границе упомянутых слоев. И все наши попытки обосновать и понять квантовые закономерности - это не что иное, как попытки проникнуть в вышележащий слой. Можно также представить как более тонкие, так и более грубые слои мироздания. Грубые слои образуются из конструктивных элементов. Так, если, например, кварк - элементарная сущность для нас, то структура из этих же частиц может казаться элементарным "кирпичиком" в некоей более грубой реальности и т.д.
Субъект-в-мире всегда создает свой слой субъективной реальности, - некий дочерний мир со своей аксиоматикой. Очевидно, что аксиоматика этого мира более примитивна, а сам мир груб. Прежде чем продолжить наш анализ, мы должны сделать небольшую паузу и поинтересоваться, помнит ли читатель о проблеме интерпретатора. Вдумчивый читатель, не страдающий забывчивостью, наверное, уже понял, что многослойная структура мира, обсуждаемая здесь, изоморфна вложенной структуре интерпретаторов, которую мы обсуждали выше. Итак, мы подошли к той же самой проблеме, но с другой стороны. В отличие от первого подхода, мы теперь имеем самосогласованную картину. Не лишним будет напомнить, что далось нам это путем отказа от первичности понятия алгоритма. Так ли уж велика цена? Едва ли, если учесть, что благодаря этому, нам удалось обрезать бесконечный ряд интерпретаторов и построить самосогласованную структуру мира. К тому же понятие алгоритма вновь возникает, но уже как субъективное. Мир для субъекта алгоритмичен, ибо субъект, всякий раз осознавая себя в одном из экземпляров мира, привносит в этот мир один из возможных способов его упорядочить. Но упорядоченность есть не что иное как алгоритм отображения множества объектов на себя.
В завершение нашего обсуждения мирового расслоения, обсудим отношения слоев между собой. Очевидно, что любому звену иерархии открыты все грубые слои и совершенно недоступны тонкие, лежащие выше него, - мы можем изменить программу в компьютере, но не она нас. Можно применить метафору- изоляции. Автомат полностью изолирован от нашего мира. И эта изоляция обусловлена бедностью его языка, неспособного отразить смыслы, возникающие во внешнем мире. С точки зрения же своего конструктора автомат не изолирован. Ведь в его власти вмешаться в программу автомата и даже остановить выполнение алгоритма.
Интересно еще рассмотреть место человека в этой структуре. На наш взгляд человек по меньшей мере трехслоен. Функция сознания обусловлена процессами в тонких слоях. Интеллект же вычислим по Тьюрингу и обусловливается процессами в "живой" машине Тьюринга. Не следует забывать и о промежуточном - физическом слое. В такой схеме человек не связан Геделевскими ограничениями внутри формальной системы его интеллекта, и этот факт мы обозначаем, как духовность, свойственную человеку. Но вполне вероятно, что сама духовность имеет ограничения типа Геделевских для расширенной аксиоматики "тонкого мира". Однако, об этом мы ничего не знаем.
Построенная картина мира несет большую эвристическую силу. Нам уже давно была известна относительность движения. Эйнштейн показал относительность времени и пространства, а позже предложил общековариантную формулировку законов природы. Эйнштейн чувствовал, что целостность мира влечет за собой относительности более высокого порядка. Однако, ему не удалось формализовать идеи Маха. Прежде всего наш подход позволяет понять, что сама реальность относительна. Если же интересоваться деталями, то простые логические рассуждения, следующие из исходного предположения о конечности мира, приводят к целому ряду относительностей - относительности бесконечного, относительности случайного, относительность разумного, а также позволяет вплотную подойти к обоснованию квантовой и статистической механики.
Рассматриваемое информационное расслоение обосновывает и придает научный смысл модному сейчас понятию виртуальной реальности. Наш мир тоже может быть некоей информационной структурой в памяти "компьютера" внешнего слоя, на котором тамошний мальчишка (Бог?) играет в одну из "стратегий".
Сознание и интерпретация Эверетта.
Сознание или свойство "быть Я" укоренено в самой основе мира. То есть это свойство самого мира, а не его части. Таким образом, бытие мира как субъект объектной целостности проявляется в форме сознания. Как мы уже говорили, субъект-объектная дихотомия априорное свойство многосущностного мира. Понимание сознания мы тесно связываем с моделью информационного расслоения, которую мы обсуждали. Субъект N-сущностного мира, как мы показали, в принципе не может наблюдать те элементарные компоненты, которые составляют его основу и основу внешних объектов. Он видит мир построенным из конструктивных элементов (таких, как "a","b","c","d" в нашем примере), которые кажутся ему элементарными (лучше сказать, являются для него таковыми). В его памяти формируется модель мира в виде грубого слоя, который он называет физической реальностью. Важно, что хотя источником сознания является "тонкий мир", смыслы, зарождающиеся в этом "тонком мире", не имеют аналогов в грубом слое и могут быть выражены только приблизительно. Мы намеренно не будем вдаваться в детали механизма смыслообразования в тонком слое, ибо это выходит за рамки настоящего схематичного изложения.
Не стоит буквально отождествлять субъект, о котором мы здесь говорим, с человеком, а грубый мир - с нашим миром. Этому грубому миру также свойственна субъект - объектная дихотомия и потому он порождает следующий по грубости слой и т.д. Одним из звеньев этой структуры является человек и его мир. Сознание же пронизывает всю эту структуру вертикально. Смыслы, возникающие в высших мирах иерархии, даются нам в непосредственном восприятии. Но, как уже говорилось, не могут быть выражены ни одним из языков, возможных в более грубых слоях (в нашем мире).
Аппарат квантовой механики может быть успешно применен и для формализации феномена сознания. Рассмотрим пространство состояний сознания (аналог Гильбертова пространства КМ). Мы его называем пространством тут-бытия. Базовые вектора этого пространства суть экзистенции - я-в-мире, ты-в-мире, он-в-мире и т.д. Вектор "Я" в этом пространстве является инвариантом, наподобие вектора квантово-механического состояния в Гильбертовом пространстве, над которым определен класс унитарных преобразований. Означает ли это, что сознание имеет квантовую природу? Возможно, да, но вероятно, что это только технический прием. Подобие всего всему, которое мы наблюдаем в мире, обусловлено не самим миром, а особенностями нашего субъективного восприятия, - мы склонны видеть сходство там, где реально его нет, ибо мы не можем заметить различие. Поэтому в этом случае, как и во многих других, где мы обнаруживаем подобие, следует проявлять особую осторожность прежде, чем отождествлять соответствующие феномены. В настоящий момент у нас нет достаточных оснований, чтобы настаивать на квантовой природе сознания. Формально акт сознания является коллапсом потенций. (Редукция вектора "Я" в одну из своих компонент). При этом Я осознаю себя конкретной личностью, оказавшейся в конкретных обстоятельствах. Описываемая здесь структура, более подробно исследуется в "Физике сознания". В связи с этим нельзя не вспомнить интерпретацию квантовой механики, которую предложил Эверетт.
Первая статья по Many Worlds Interpretation (MWI) была опубликована Эвереттом в 1957 г. Целью этой работы было разрешение парадокса Эйнштейна-Подольского-Розена (EPR).
Решение Эверетта состоит в утверждении, что реализуются все возможности, но при этом система субъект-объект обзаводится "двойниками", принадлежащими различным мировым экземплярам. Иногда говорят "листам" или "ветвям". Каждый лист соответствует одному из членов общей волновой функции, описывающей мир в целом. Наблюдатель, находящийся на одном из листов, не в состоянии обнаружить существование других листов. Наша модель мира имеет много общего с этим представлением Эверетта. Такая интерпретация позволяет успешно избежать мгновенного коллапса волновых функций на всем пространстве, но при этом вводит множество ненаблюдаемых параллельных миров. Копии наблюдателя присутствуют на каждом из этих листов. На каком именно из листов обнаруживает себя наблюдатель наделенный сознанием? Почему, делая выбор, я становлюсь свидетелем и участником только одной возможности?
Часто можно слышать, что этот вопрос относится больше к философии и психологии, чем к физике. Однако, если мы хотим включить сознание в ткань физической теории, мы должны уметь отвечать на этот вопрос. Переформулируем этот вопрос следующим образом. На что, или на какие направления проецируется вектор "Я" в акте сознания. Рассмотрим базовый набор состояний сознания Я1, Я2, - ЯN или базовый набор направлений в пространстве тут-бытия. Возможно, конечно, рассматривать конечное число различных ортогональных базисов, образованных путем линейного комбинирования векторов Я1, Я2, - ЯN. В принципе возможно рассматривать любой базис, так как конкретные актуализации сознания (тут-бытие) - отдельные компоненты "Яi" не имеют статуса реальности. Реальна только их совокупность (в любом базисе), определяющая инвариант "Я".
И все же, на что проецируется "Я"? Чтобы это понять, можно рассмотреть функциональное пространство. Например, разложение некоторой гармонической (что бы базис тоже был конечномерный) функции в ряд Фурье. Тогда относительно любой компоненты разложения можно спросить, проекцией на что она является? Формально, она является проекцией на направление, отождествляемое с какой-либо гармоникой (например, sin7ωt). Мы полагаем, что инвариант "Я" можно понимать, как некоторую функцию, которую вычисляет мировой алгоритм. Личности или состояния сознания "Яi" - части (подпрограммы) общего мирового алгоритма.
Допустим, что все это так, скажете вы, но что является причиной коллапса "Я" в одну из своих компонент? Может быть, это нехорошо, но иногда бывает удобно задать контрвопрос. Поэтому я спрошу- что является причиной коллапса какого-либо КМ состояния? Наличие наблюдателя - это не причина коллапса, а необходимое условие. Сама редукция ВФ происходит спонтанно. Здесь есть две точки зрения: 1) причина есть - это идеология скрытых переменных, и 2) причины нет - это Копенгагенская интерпретация. Мы придерживаемся первой и считаем, что такая причина есть, но она скрыта от субъекта в силу ограниченности его возможностей в конечном мире (пример с 6-битным миром). В нашей модели имитирующей квантовые корреляции, приведенной в главе "моделирование и реальность" выбор одного из возможных состояний при коллапсе осуществляется генератором псевдослучайных чисел. Но для субъекта (пользователя) механизм этого выбора недоступен. Поэтому для него он истинно случаен, хотя для внешнего наблюдателя, имеющего доступ ко всем ресурсам компьютера (скрытым переменным), очевидна детерминированность этого выбора. Таким образом, причина коллапса, а с ней и результат любого измерения локализованы в недоступном для субъекта (вследствие неполноты) слое мира. Но эту возможность совершенно естественным образом предоставляет наша модель! Аналогично этому, причина акта сознания, приводящая к осознанию мною себя конкретным человеком среди людей, укоренена в нашей сфере субъективного.
Напомним, что мы помещаем сферу субъективного в тонкий слой иерархии мироздания, недоступный субъекту вследствие его (субъекта) физической "неполноценности" (у него просто не хватает битов (шариков!) для отражения богатой реальности "тонкого мира"), поэтому смыслы, возникающие в субъективном слое, будучи недоступны для рефлексивного развертывания на языке ментального слоя, даются нам в непосредственном восприятии. Поэтому можно сказать, что решение о коллапсе принимает сам субъект, но не всегда знает об этом, ибо здесь работает подсознание, а если даже и знает, то не всегда может объяснить свое решение.
"Война и мир" и Q-логическая глубина.
Пытаясь понять причины спонтанного роста порядка и усложнения форм материи в отдельных частях Вселенной, например, эволюцию жизни и нашего знания, физики обычно используют такой критерий, как энтропия. Математики предпочитают другой критерий порядка, называемый сложностью. Как известно, порядок и хаос понятия относительные. А.Н.Колмогоров, Г.Чейтин и Р.Соломонов независимо друг от друга определили сложность K(n) n значной последовательности, как длину в битах самой короткой программы, вычисляющей эту последовательность на универсальной МТ. Позже Беннет, а затем и Дойч исследовали аналогичную меру сложности, называя ее "логической глубиной". Для квантовых вычислений Дойч предложил термин "Q-логическая глубина".
Так как мировое состояние может быть выражено словом длиной N, то можно говорить о сложности этого состояния. Среди этих состояний есть такие, которые могут быть вычислены программой длиной K(n)<N. Такие состояния могут быть плодом деятельности субъекта. То есть они могут быть искусственными формами. Но есть и состояния с K(n) ≥ N. Такие состояния обычно относят к совершенно случайным, а последовательности знаков их выражающие - невычислимыми. Возникает вопрос - как отличить довольно сложное, но случайное состояние от конструктивного? Или не может ли (совершенно случайно!) случайная последовательность оказаться неслучайной? Для бесконечных последовательностей П. Мартин-Леф ввел более сложный критерий в виде предела, к которому стремится отношение K(n)/n при n - ∞. Однако, для конечных последовательностей, по-видимому, в этом нет необходимости. Понятия случайности как такового нет в нашей модели. Однако, максимально-сложные состояния, удовлетворяющие критерию K(n) ≥ N можно формально назвать случайными, хотя бы в том смысле, что их экзистенциальный статус уже никак не может быть связан с субъектом.
Традиционное представление о мире не позволяет понять, как могла возникнуть столь большая логическая глубина, чтобы развить Ψ, соответствующие, например, роману Толстого "Война и мир" или сверхзвуковому лайнеру "Конкорд", не говоря уже о биологической эволюции живого. Мы же на этот вопрос даем очень простой ответ. Состояние Ψ, соответствующее роману Толстого "Война и мир", как одно из мировых слов, понятных субъекту, всегда существовало. Его просто не могло не быть, ибо это одно из слов, составленных в N буквенном мировом алфавите. И это слово выражает относительный субъективный смысл, как то "Конкорд", "мозг" или роман Толстого. Заметим, что с точки зрения внешней мета-реальности такая "штука", как "Конкорд" совершенно бессмысленна. Вопрос - почему мы стремимся к познанию или почему имеет место эволюционное развитие - некорректен. Актуально существует весь спектр степеней познания мира и вся лестница эволюции. Почему мы вновь и вновь удивляемся очевидному? Ведь прошло уже почти 100 лет с тех пор, как Минковский, следуя Пуанкаре, глубоко осознал, что только единый 4-х мерный мир пространства-времени может иметь статус реальности, тогда, как время и пространство, взятые сами по себе, довольно эфемерные сущности. Выступая в 1908 г с докладом перед естествоиспытателями и врачами, Минковский говорил: "Милостивые господа! Воззрения на пространство и время, которые я намерен перед вами развить, возникли на экспериментально-физической основе. В этом их сила. Их тенденция радикальна. Отныне пространство само по себе и время само по себе должны обратиться в фикции, и лишь некоторый вид соединения обоих должен сохранить самостоятельность". Нельзя не процитировать в связи с этим и фрагмент из лекции Вейля, прочитанной им в 1933 г. "-Объективный Мир, пространство-время только существует, а не происходит; как целое он не имеет ни какой истории. Только перед взглядом сознания, поднимающегося по моей мировой линии, сечение этого мира "оживает" и движется мимо, как пространственный образ, подвергаемый временному преобразованию".
Вместо заключения.
Возвращаясь к началу этой статьи и к эпиграфу, взятому из знаменитой работы гениального ученого, скажу, что сам Вейль здесь немного лукавит, ибо кто как не он сам черпал свое математическое вдохновение, читая Гуссерля и Фихте. И кто как не он осуществлял массированную экспансию математической мысли в области, традиционно считавшиеся принадлежащими философии. Хочу добавить для тех читателей, кто был разочарован отсутствием в наших рассуждениях математической строгости, что предметом нашего исследования являлся поиск той базовой системы понятий и категорий, на основе которой могла быть построена самосогласованная картина алгоритмического мира. Легко понять, что эта задача в принятой нами постановке изоморфна труднейшей задаче обоснования математики. Но замкнутый и самосогласованный математический мир до сих пор не построен и мы не знаем, возможно ли это. В основе любой математической теории всегда лежат некие привносимые извне сущности, смысл которых образован внутри слоя нашей субъективности. И это будет иметь место до тех пор, пока само сознание не будет включено в конструкцию математического здания. Было бы наивно думать, что здесь мы в полной мере реализовали этот замысел. То, что мы сделали - это только наброски, подготавливающие идеологическую основу, попытка постановки задачи. Поэтому, если эти идеи найдут отклик у какого-нибудь смелого и азартного математика, который отважится отвоевать у философии еще пядь земли, мы будем считать, что поставленная нами задача выполнена.
Итак, возможно ли алгоритмическое описание мира? Вопрос пока остается открытым.
Я хочу поблагодарить Исупова И. обратившего мое внимание на противоречивость исходных посылок в работе "Алгоритмическая модель мира" и тем самым стимулировавшего написание настоящей работы, Полосухина Б.М. за интересные дискуссии о роли сознания в мироустройстве, а так же за чтение черновика и ряд замечаний, оказавших незаменимую услугу в процессе написания статьи.
Список литературы.
[1] David Deutsch. «Quantum theory, the Church-Turing principle and the universal quantum computer». Appeared in Proceedings of the Royal Sciety of London A 400, pp. 97-117 (1985)
[2] А.В.Каминский Алгоритмическая модель мира.
[3] A.Peres (1993), «Quantum Theory: Concepts and Methods», Kluwer Academic Publishers.
[4] P.SHOR, «Algorithms for quantum computation: discrete log and factoring», Proceedings of the 35th Annual Symposium on the Foundations of Computer Science, S.Goldwasser (editor), IEEE Computer Society Press, Los Alamitos, 1994, pp. 124-134.
[5]
A.Barenco, A.Ekert, A.Sanpera, C.Machiavello
«A Short introduction to quantum computation» www.qubit.org
[6] R.Feynman «Simuating Physics with Computers», Department of physics, California Institute of Technology,Pasadena, California 91107
[7] Einstein A., Podolsky B., Rosen N. - Phys. Rev., 1935, v.47, p.7
[8] Г.Вейль. «Математическое мышление»: М.: Наука., 1989. Стр.103
Другие работы автора на сайте digitalphysics.ru
Каминский А.В. Этюды о неполноте // LAP Lambert Academic Publishing. 2016.