Квантовая Магия, том 5, вып. 4, стр. 4121-4131, 2008
Механика квантовой механики
А.В. Каминский
(Получена 23 августа 2008; опубликована 15 октября 2008)
Эта статья адресована тем, кому интересно знать, почему механика – квантовая.
Если вообразить себе время как прямую линию, протянувшуюся из прошлого в будущее, то наше сознание можно рассматривать как колесо,
катящееся вдоль этой линии и касающееся ее только в одной точке.
С. Лемм.
Введение
Квантовые состояния можно определить, как принципиально различимые состояния системы. Например, согласно принципу неопределенности Гейзенберга, в фазовом пространстве хорошо различимы ячейки с объемом Δp Δx~h/2π где h - квант действия. Говоря фигурально это - объем квантового состояния. Если фазовый объем системы мы разделим на объем одного квантового состояния, то получим число квантовых состояний. Физические системы с конечным объемом и энергией имеют конечное число квантовых состояний. Если мы разделим фазовое пространство на меньшее число частей, то эти части уже не будут независимы и образуют квантовые суперпозиции. Является ли квантовое состояние первичным элементом реальности? С одной стороны – да. Нам трудно говорить о его структуре. Например, система не имеет определенных координат и импульсов внутри Δp Δx. Можно даже сказать, что она вообще не имеет этих свойств внутри ячейки (до измерения). А раз так, то едва ли имеет смысл говорить о структуре этой ячейки. С другой стороны, квантовое состояние характеризуется фазой, и это свидетельствует о его конструктивности. Квантовые состояния с разными фазами при сравнении их в интерферометрических опытах проявляют свое относительное отличие. А это означает то, что имея дело с квантовым состоянием, мы на самом деле имеем дело со структурой - классом неких более фундаментальных состояний. Математически этот факт выражается в том, что квантовым состояниям в гильбертовом пространстве соответствуют не точки, а лучи, или же классы пропорциональных комплексных функций. В известном смысле слова, эти фундаментальные состояния можно назвать – скрытыми состояниями, так как мы их не различаем. Мы хотим вновь обсудить идею о том, что квантовая механика, описывающая поведение объектов нашего мира возникает, как следствие неполного знания наблюдателя о них. Однако, неполнота, о которой мы будем говорить, не является математическим приемом, подобно тому, который используется в статистике. Рассматриваемая нами неполнота носит фундаментальный характер и в моделях конечного мира находит обоснование в теоремах К.Геделя.
В основу предлагаемого анализа положена гипотеза о существовании субквантового уровня организации материи. Динамика мира на этом уровне реальности подчиняется локально детерминистическим законам. Современный скепсис к локальному реализму обусловлен слишком прямолинейным пониманием такой возможности. Мы покажем, что локальный реализм на фундаментальном уровне организации материи не только не противоречит квантовой теории, но возможно лежит в ее основе.
1. Физическая неполнота и запутанные состояния
Рассмотрим систему, имеющую конечное множество M локально-связанных состояний. То есть мы предполагаем существование некоей функции ξ отображающей это множество на себя ξ:M<--M. Траектории такой системы в пространстве ее состояний эргодичны и представляют собой конечные циклы. Любые части этой системы, очевидно, имеют циклы не большей длины.
Выделим из системы 2 части, соответствующие – наблюдателю (субъекту) и исследуемому объекту. Будучи частями единого "большого" цикла, эти подсистемы испытывают некоторое согласованное изменение состояний.
Для большей наглядности мы воспользуемся механистической метафорой механизма. Такие наглядные образы часто бывают полезны при построении теории, но сослужив службу впоследствии оказываются ненужными,- их роль берет на себя математический формализм.
Рассмотрим систему, состоящую из двух подсистем - шестерней. Каждый зубец шестерни "Subj" соответствует состоянию наблюдателя, а каждый зубец шестерни "Obj" - состоянию объекта. Объектом может быть любая часть Вселенной, исключая наблюдателя.
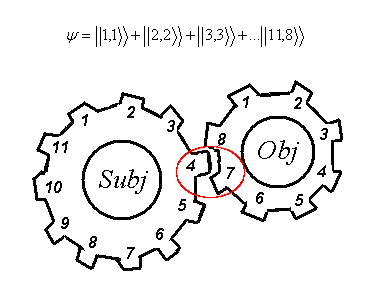
Рис.1.
Механическая зацепленность шестерней имитирует зацепленность квантовых состояний.
Следует остерегаться слишком прямолинейной интерпретации субъекта, как конкретного экспериментатора (наблюдателя). В такой постановке возникает проблема, связанная с существованием множества наблюдателей с разным числом состояний, приводящая к ряду противоречий. Учитывая, что проблема наблюдателя в рассматриваемой модели не решена, предлагается временно абстрагироваться от множественности субъектов, и считать, что существует только один субъект – наблюдатель с числом состояний NS. Наша квази-механическая модель иллюстрирует Эвереттовские соотнесенные состояния [1]. Но это - классический аналог соотнесенных состояний (далее мы будем употреблять современный термин – зацепленные или запутанные состояния). Принципиальным отличием является то, что состояния нашего механизма вовсе не квантовые. Ведь мы за основу взяли состояния, понимаемые в локально-детерминистическом аспекте. В дальнейшем мы отождествим их с некими фундаментальными (субквантовыми) состояниями. Итак, мы предположили, что зубья шестеренки "Subj" – суть состояния наблюдателя, отвечающие за его знание о наблюдаемой системе. Число этих состояний - NS. Число состояний объекта (шестеренка "Obj") обозначим - N0. Число конфигурационных состояний системы наблюдатель - объект будет:
![]() ;
(1)
;
(1)
НОД – наибольший общий делитель чисел состояний. Если числа NS; N0 кратны, то число состояний составной системы равно наибольшему из этих чисел. Другой крайний случай имеет место, если эти числа взаимно простые. Тогда число состояний системы равно их произведению. Это следует так же из того, что прямое произведение двух циклических групп Z/n and Z/m является циклической группой только в том случае, если n и m взаимно простые. Состояния составной системы (конфигурационные состояния) будем выражать парой номеров зубьев в точке сцепления. Например, на рисунке 1 система находится в состоянии ||Ψ>>=||>4>||>7>. Для отличия от Дираковских обозначений квантовых состояний системы мы, для обозначения фундаментальных состояний, используем двойные угловые скобки. Понятно, что состояния ||i>> и ||j>> i≠j , относящиеся к одной и той же шестерне ортогональны <<j||i>>=δij, так как система не может находиться в двух состояниях одновременно.
Состояния ||i>>||j>> и ||i+k>>||j>> субъект различает по определению, а состояния ||i>>||j>> и ||i>>||j+k>> не различает, так как этим состояниям системы соответствует одно и то же состояние ||i>> наблюдателя. Здесь k=1,2,3…, а счет в каждой из скобок идет по модулю NS и N0, соответственно. Из дальнейшего будет ясно, что этим состояниям соответствуют разные фазы ВФ или, что то же самое, разные точки на луче в Гильбертовом пространстве состояний системы. Из (1) следует, что зацепление систем "Subj" и "Obj" может только уменьшать число состояний составной системы. Незацепленные шестерни вращаются произвольным образом, и состояние такой системы, можно назвать факторизуемым.
Число состояний системы с взаимно-простыми NS; N0 равно числу состояний системы с незацепленными состояниями. Система представленная на рисунке 1 имеет 88 состояний, так как числа 11 и 8 взаимно простые. Функцию, характеризующую запутанное состояние рассматриваемой системы запишем в виде:
ψ(j)=||i+j>>||j+k>> (2)
i и j – некоторые начальные значения. Мы предполагаем, что все процессы ("колесики") во Вселенной зацеплены. Независимые (факторизованные) процессы это только лишь приближение, которое применимо к системам, связь между состояниями которых скрыта от субъективного наблюдателя и не прослеживается явно.
Здесь мы, в некотором смысле, возвращаемся к истокам механики, когда вся Вселенная представлялась нам одним грандиозным механизмом. Однако, не было бы причины для обсуждения этой старой идеи, если бы в нее не вкладывалось понимание того очевидного, но упорно игнорируемого факта (даже после появления в 1957 г основополагающей работы Эверетта по соответственным состояниям [1]), что наблюдатель в самом широком смысле этого слова, всегда является частью Вселенной, которую он изучает.
В наиболее общем случае числа состояний наблюдателя и объекта не кратны:
NS=kN0+res (3)
Если N > NS то, состояния субъекта вырождены. Степень вырождения обозначим: ξ=N/NS. В нашем примере ξ=8. Вырожденность состояний субъекта отражает принципиальную ограниченность его "когнитивных" возможностей. Это означает, что имеются различные состояния системы, которые субъект воспринимает, как одно состояние. Число состояний субъекта не достаточно для того чтобы взаимно – однозначно сопоставить им конфигурационные состояния составной системы. Эту ситуацию мы называем физической неполнотой [2], [3], [4]. Если ее обобщить, то мы должны признать существование скрытых процессов и объектов, которые не могут быть обнаружены непосредственно, но по всей видимости, должны проявлять себя косвенно в физических закономерностях, управляемых движением видимой части материи. Мы не станем искать референт этой скрытой части реальности (им, например, может оказаться темная материя), ибо это выглядело бы спекуляцией.
Вернемся к нашей модели. При вращении зацепленных шестерней система последовательно перебирает состояния ξk={||i+k>>||j+k>>}. Так опишет ситуацию объективный наблюдатель, то есть некоторый метанаблюдатель, способный распознать каждое состояние системы в каждый объективный момент времени и описать полную картину происходящего. Иногда мы будем называть такого наблюдателя - внешним или сторонним наблюдателем, то есть это наблюдатель не являющийся частью системы и имеющий число состояний не меньшее числа состояний системы. Для нашей квази-механической модели таким наблюдателем мог бы быть механик, проверяющий хорошо ли сцеплены шестерни в часовом механизме. Но, если речь идет о мировом "механизме", то представление о таком наблюдателе сродни представлению о демоне Лапласа.
Для субъективного наблюдателя все выглядит иначе. Механика, которую он построил бы для описания его субъективной реальности, неизбежно содержала бы элемент неполноты. Действительно, число состояний такого наблюдателя не достаточно для того, чтобы он мог составить полное, однозначное представление о системе. В нашем примере (Рис.1) наблюдатель имеет только 11 различимых (8-кратно вырожденных) состояний. Представим "фазовую" траекторию системы в координатах степеней свободы субъекта (наблюдателя) и объекта (остальной части мира).
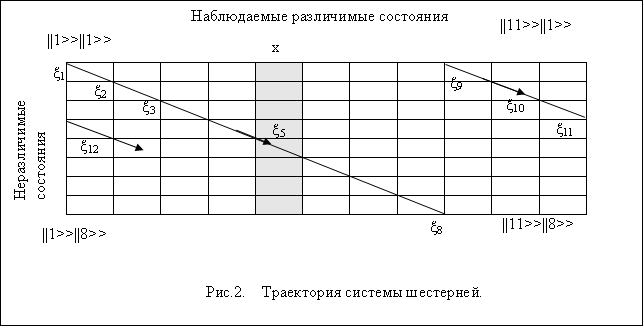
По оси x здесь отложены состояния наблюдателя, ответственные за наблюдаемое свойство объекта. Так, если объект находится в точке x, то его состояние в Дираковских обозначениях |x>. В нашем примере это состояние 8-кратно вырождено по фундаментальным состояниям. Для субъективного наблюдателя все выглядит, так, как если бы имелась некая скрытая добавочная степень свободы.
Легко видеть, что, подобно системе двух связанных осцилляторов, фазовое пространство состояний рассматриваемой квазимеханической системы представляет собой многообразие тороидальной топологии T2. На Рис.2 изображена развертка тора (Противоположные стороны отождествлены). Фазовая траектория системы является геодезической (локсодрома) на торе. На плоском торе возможны 3 класса траекторий в соответствии с числом топологической связности. Подобные структуры часто встречаются в физике [5]. В непрерывном приближении формула 2 имеет вид: Ψ = exp(ix)exp(ixh). Где x и xh являются функциями объективного времени tObj. Это выражение является решением уравнения движения системы двух связанных осцилляторов, которое, как известно, в фазовом пространстве, описывается многообразием тороидальной топологии. В нашем случае мы имеем тор T3 в пространстве (xi,xih,t,th). Разбив Вселенную на 2 части (субъект - объект) мы предельно упростили картину. Однако, она позволяет понять основные принципы нашего подхода называемого субъективной физикой.
Введем время, как поток событий смены состояний системы. Поворот системы шестерней на один зубец соответствует одному кванту времени. В общем случае, порядок смены состояний может определяться неким алгоритмом. Поэтому мы будем называть это время алгоритмическим, а фазовую траекторию системы – алгоритмической траекторией. Таким образом, мы исходим из предельно простой алгоритмической картины - мир, как конечное множество состояний (которое разбивается на подмножества субъекта и объекта) плюс, действующую над ним, функцию отображения этого множества на себя. В такой системе, как мы показали выше, для субъекта имеет место ситуация неполноты, приводящая к необходимости рассматривать 2 масштаба времени. Наблюдаемое физическое время (субъективное) и алгоритмическое (или объективное время). Полный период системы в приведенном примере (время между "возвратами Пуанкаре") составляет TObj = 88 квантов алгоритмического времени. Полный период наблюдателя равен TSubj =11 квантам физического времени. Таким образом, каждый субъективный квант содержит 8 скрытых квантов времени. Как видим, наша модель вполне естественно приводит к понятию скрытого времени, которое вводят феноменологически в ряде интерпретационных моделей КМ. В последнее время к этому понятию все чаще прибегают разные исследователи [6][7].
Что это означает физически? Как мы уже говорили, для внешнего наблюдателя поворот шестерни Subj на один зубец является событием перехода к следующему моменту алгоритмического времени. Для наблюдателя, связанного с этой шестерней (который, согласно модели, ею и является), событием может быть только встреча с определенным зубцом другой шестерни. Рассмотрим эту ситуацию подробнее. Пометим зубец на шестерне Obj. Движение такой метки может описывать движение частиц, например, фотона. Следует обратить внимание на то, что если бы наблюдатель мог определить фазу движения частицы (угол поворота шестерни Obj φ=n*2π/8 ), то в совокупности со своими apriori доступными 11 состояниями, ему были бы доступны все 88 состояний системы, чего, как мы уже говорили, быть не может. Поэтому, абсолютное значение фазы не может быть доступно субъекту. Различимыми физическими событиями следует считать только события встречи помеченного зубца шестерни Obj с шестерней Subj. Только это событие следует считать переходом к следующему моменту физического времени. В промежутке времени между этими событиями положение частицы, хотя и имеет в каждый момент объективного времени вполне определенные значения, для субъективного (физического) наблюдателя в принципе неопределимо. Частоту, с которой наблюдатель встречается с частицей-меткой нужно интерпретировать, как энергию (минимальная порция энергии (квант) равна ΔE=1/TSubj). Тогда время и энергия – сопряженные переменные, связанные преобразованием Фурье на конечном базисе. Поэтому точность задания одной из них влияет на точность другой, что формально соответствует принципу неопределенности. Циклическая природа самого наблюдателя в нашей модели приводит к эффекту "стробоскопа", на основе которого легко понять причину квантования энергии. Например, наблюдая через стробоскоп за классическим осциллятором с непрерывным спектром энергии, мы обнаружили бы наличие дискретного ряда стационарных состояний с кратными частотами.
Итак, мы показали, что для наблюдателя, состояния которого формально определены на подмножестве конечного множества Ω мировых состояний, возникает ряд ограничений и специфических свойств, характерных для квантовой механики.
2. Природа комплексных чисел
Как известно, аппарат КМ формулируется на комплексном поле, тогда как в основе рассматриваемой модели лежит дискретное конечное поле. Существует ли связь между этими описаниями?
Пусть S конечное множество фундаментальных состояний мира. И пусть R биективное отображение этого множества на себя R:S->S. Такое отображение порождает несвязанные циклы. Каждый цикл может рассматриваться, как отдельная "вселенная" никак не связанная с другими. Поэтому нас будет интересовать любой отдельный цикл, состоящий из N состояний, который мы отождествим с нашей Вселенной. Например, цикл состояний механизма Рис.1. Однозначная связь элементов в цикле позволяет ввести линейное алгоритмическое время и определить на нем Мировую Функцию ψ(tO), задаваемую отображением R. В общем случае, такой цикл образует алгебраическое кольцо. В частном же случае, когда число элементов простое - поле Галуа. Если наша Вселенная конечна, то геометрия и алгебра на конечных полях должны быть естественным языком для описания физики, тогда как традиционный дифференциальный аппарат, построенный на действительном комплексном поле, может быть только удобным асимптотическим приближением. В связи с этим интересно отметить, что комплексное поле можно рассматривать, как расширение поля Галуа. Возможно, что этот факт является намеком на то, что квантовые закономерности унаследовали "комплексность" от первичного конечного поля, лежащего в основе нашего мира. В качестве простого примера построим комплексное расширение поля GF(23). На этом поле имеем:
02=0; 12=1; 22=4; 32=2; 42=2; 52=4; 62=1, а значит, числа 3,5,6 являются квадратичными невычетами. На действительном поле, где отрицательные числа играют роль квадратичных невычетов, формально вводят комплексное расширение i2=-1. В случае поля Галуа это расширение можно ввести более осмысленно. Для этого достаточно заметить, что при счете в обратном направлении ситуация меняется на обратную – числа 1,2,4 становятся квадратичными невычетами, а для чисел 3,5,6 находятся квадраты. Обозначая направление счета буквой i, как атрибут числа, имеем: i2=6(-1); (2i)2=3(-4); (3i)2=5(-2); (4i)2=5(-2); (5i)2=3(-4); (6i)2=6(-1).
Таким образом изменение знака алгоритмического времени, изменяющее направление движения на поле Галуа эквивалентно комплексному сопряжению. Наверняка эта ситуация покажется читателю знакомой. Действительно, в квантовой механике вектор состояния так же связан с направленностью времени. Это очевидно при рассмотрении оператора обращения времени:
![]() Ψ(
Ψ(![]() ,t)
= Ψ*(
,t)
= Ψ*(![]() ,-t)
(4)
,-t)
(4)
Для сохранения инвариантности относительно операции обращения времени необходимо одновременно осуществить комплексное сопряжение. Этот факт (то, что комплексное сопряжение эквивалентно обращению времени), весьма загадочный в квантовой механике, на расширенном поле Галуа тривиален.
Учитывая сказанное, Функция ψ(t), задаваемая отображением R может быть записана в виде
ψ(t)=1·eiωt (5)
Известно, что комплексная алгебра изоморфна минимальному представлению алгебры Клиффорда – это алгебра матриц поворота на плоскости. Действительно, комплексное число r=a+bi на самом деле можно понимать, как сокращенную запись следующего выражения:
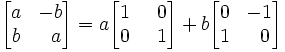
Мы считаем, что глубокая укорененность комплексных чисел в квантовой механике свидетельствует именно о циклической природе описываемой ею реальности. Как известно, комплексные функции часто для удобства (с известной избыточностью) используются для описания периодических процессов. Таким процессом, например, является изменение давления в звуковой волне. Скалярные периодические процессы, в отличие от циклических движений по замкнутому пространственному контуру, описываются действительными периодическими функциями. Часто подчеркивают особенную роль комплексных чисел в квантовой механике. "В квантовой механике", - как пишет Крамер [8], - "комплексные функции "проглатываются" целиком". Не оспаривая этот факт, заметим, что при описании вращения, и в классической механике, совершенно необходимы комплексные функции! По всей видимости, объектом КМ являются именно циклические движения на субквантовом (скрытом вследствие неполноты) уровне организации материи.
3. Субъективная перенормировка времени и возникновение квантовых состояний
Рассмотрим снова мировую эргодическую функцию (2). Номер состояния k мы будем интерпретировать, как алгоритмическое время t. На области определения t ⊂ {0,T0} ее значения никогда не повторяются Ψ(t1) ≠ Ψ(t2) для всех t1 ≠ t2. К таким функциям относятся, только монотонные функции или разрывные функции специального вида. Представим ее подобно (2) в факторизованном виде:
Ψ = Ψ S Ψ 0
Соответственно, размерность функционального пространства мировой функции ψ равна тензорному произведению пространств состояний субъекта и объекта. Очевидно, что субъективная (относящаяся к субъекту) часть ΨS этой функции уже не будет эргодической и ее значения на области t ⊂ {0,T0} неизбежно повторяются с периодом T0'=T0/ξ. Так как состояния в каждом цикле идентичны, это означает, что для физического наблюдателя значимым будет только период времени T0' . То есть при переходе к физической (наблюдаемой) картине мира, мы должны перемасштабировать время t → t/ξ. Диапазон характерных времен при этом сужается, а число ячеек фазового пространства, уменьшается в ξ раз. Так в нашем примере на Рис.2, при переходе к субъективному наблюдателю, число ячеек уменьшается с 88 до 11. Формально, переход к субъективному наблюдателю является редукцией к пространству меньшей размерности. Такой переход приводит к сокрытию от наблюдателя части информации о системе (неполнота). При условии достаточной детализации модели, для расчета наблюдаемых, возможно, окажется полезна техника ренорм-групп. Однако, мы здесь ограничимся лишь этим замечанием.
Учитывая периодичность ψ функции (объективное представление) составной системы по алгоритмическому времени tO, разложим ее на конечном базисе Фурье:
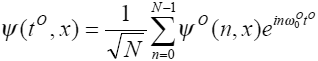 (6)
(6)
Ограничим класс возможных функций, определив весовые коэффициенты на двоичном поле Ψ0(n,x)∈{0,1}. Этот искусственный прием оправдывается элементарностью процессов на объективном (субфизическом) уровне реальности (*).
Переходя к физическому времени (к субъективному представлению) мы должны
сгруппировать в (6) члены суммы с близкими частотами неразличимыми субъектом
(неразличимость обусловлена принципиальным отсутствием у него средств для измерения времен
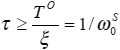 ).
Новый редуцированный базис, полученный после перенормировки, есть ничто иное,
как базис Гильбертова пространства физических состояний.
Разложение по физическому базису:
).
Новый редуцированный базис, полученный после перенормировки, есть ничто иное,
как базис Гильбертова пространства физических состояний.
Разложение по физическому базису:
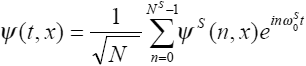 (7)
(7)
Здесь уже идет суммирование по хорошо различимым - квантовым состояниям ΨS. Таким образом чистые квантовые состояния являются классами субъективно неразличимых состояний. Мы можем легко определить вероятность физического состояния, как неотрицательную аддитивную нормированную меру, заданную над Булевой σ-алгеброй [9] классов объективных состояний (В традиционной σ-алгебре это – события £ на множестве элементарных исходов Ω). Учитывая, евклидовость метрики Фурье, а так же то, что коэффициенты мы определили на двоичном поле Ψ(n,x)∈{0,1}, вероятностная мера может быть определена, как мощность класса объективных состояний. Действительно, ψS=√ξ(x), где ξ(x) - степень вырождения состояния "x". При этом проекционный постулат фон-Неймана, описывающий переход к вероятностям, становится очевидным следствием модели. Действительно, вероятность определяется просто степенью вырождения данного физического состояния и вычисляется, как скалярное произведение P=ξ=ΨΨ*.
Таким образом, переход к субъективному наблюдателю описывается перемасштабированием времени, и приводит к тому, что единый алгоритмический процесс распадается на неразличимые циклы (процессы), составляющие "вес" или "амплитуду" квантового состояния (переход от (6)→(7)). В КМ аргументом комплексных чисел кодируются степени вырождения, а фаза, как мы показали, может интерпретироваться чисто кинематически, как фаза циклического процесса, например, движения частицы в скрытом времени.
Вследствие перенормировки, единый цикл объективно-детерминированного движения частицы, распадается на ряд не связанных (с точки зрения субъективного наблюдателя) циклов с разными (субъективно неразличимыми) фазами. Возникает поле частиц двойников. При измерении, когда одна из частиц пакета попадает в «капкан» детектора, весь пакет «схлопывается», так как на объективном уровне реальности имеет место всего одна частица, совершающая циклическое движение. Квантовая теория постулирует процесс редукции, не вникая в суть явления. На основе этого подхода может быть сформулирована оригинальная квантово-полевая концепция:
Квантовое поле производно от частиц и возникает в результате неполноты восприятия времени наблюдателем (субъектом).
Покажем, что описанная выше картина физической реальности является особой формой Эвереттовского мультиверса.
4. Временной мультиверс
Рассмотрим простейший мысленный эксперимент. Источник света излучает отдельный фотон (Фоковское состояние с примесью вакуума), который направляется на полупрозрачную пластинку, установленную под углом 45º. С точки зрения субъективного наблюдателя вероятность того, что фотон проходит через пластинку 50%. Такая же вероятность его отражения. В интерпретации Эверетта в процессе измерения мир расщепляется на 2 параллельных одновременно существующих альтернативных мира. Как известно, такая интерпретация не дает ответ на вопрос о том, почему я оказался, например, в том мире, где фотон прошел через пластинку, а не в том, где он отразился от нее. И, хотя этот вопрос не совсем физичен, он оставляет неприятное ощущение незавершенности теории. Покажем, что наша модель эффективно снимает вопрос выбора альтернатив.
Рассмотрим подробнее, как возникает картина мультиверса в модели субъективной физики. Как мы уже обсуждали, алгоритмическая (фазовая) траектория мира замкнута, и состояния мира периодически воспроизводятся. То есть имеют место возвраты Пуанкаре. Возвраты же наблюдателя в одно из своих прежних состояний (включая память!), по понятной причине происходят значительно чаще, чем возвраты всей системы в свое исходное состояние. Назовем их субъективными возвратами Пуанкаре. За время одного цикла существования Вселенной TObj реализуется ξ субъективных возвратов Пуанкаре с периодом TSubj. Однако, эти состояния принципиально не различимы наблюдателем и, следовательно, воспринимаются им, как один и тот же момент физического времени. Мы видим, что субъективное время наблюдателя, на самом деле, должно иметь довольно сложную структуру - его "Я" существует одновременно в разные эпохи, сшиваемые сознанием в картину актуально существующего настоящего (см. рисунок 3).
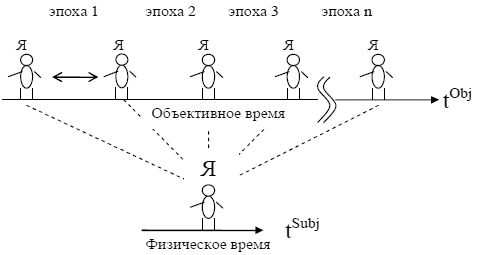
Рис.3.
Вернемся к нашему эксперименту. Пусть наблюдатель обнаружил, что фотон прошел через пластинку. Это может означать, что в одну из прошлых эпох, отделенных от настоящего момента трансфинитным (для субъекта) промежутком времени, в «том же самом» эксперименте реализовалась другая возможность (фотон отразился от пластинки).
Таким образом, в нашей модели возникает расслоение мира, подобное Эвереттовскому, но это расслоение во времени. Мировые листы (объективно) здесь существуют не одновременно. Мы называем их Эвереттовскими эпохами. На объективном уровне реальности, не доступном наблюдателю, эпохи причинно упорядочены на линейном алгоритмическом времени. Поэтому, физический наблюдатель последовательно реализует все возможности. Для него эквидистантные промежутки алгоритмического времени, названные нами эпохами, неразличимы и, поэтому, проецируются на один и тот же интервал на шкале физического времени, который мы должны отождествить с физическим временем жизни физической (субъективной) Вселенной. В терминах теории расслоений - эпохи образуют слои скрытого времени, а физическое время является базой в структуре этого расслоения.
Выводы
1. Детерминизм на фундаментальном уровне реальности в рамках конечной модели вырождается в специфический квантовый индетерминизм
2. По крайней мере в некоторых случаях, конечные поля имеют комплексное расширение и в пределе изоморфны комплексному полю на котором строится КМ. Эквивалентность комплексного сопряжения – обращению времени на конечных полях имеет тривиальное происхождение. Показано, что в рамках рассматриваемой модели находит решение КМ загадка комплексности. Ответ состоит в циклической динамике на фундаментальном конечном поле.
3. Вероятность в модели может быть определена, как мера на σ-алгебре классов фундаментальных состояний. Показано, что, в рамках рассматриваемой модели, проекционный постулат фон-Неймана находит естественное обоснование.
4. В рамках рассмотренной модели, понятие поля является вторичным и возникает из обычной механики при субъективной перенормировке времени (при переходе к физическому наблюдателю).
Литература
1. Everett H. III, Rev. Mod. Phys. 29, 454 (1957).
2. Каминский А.В. Моделирование физики в условиях неполноты. Квантовая Магия, том 1, вып. 3, стр. 3126-3149, 2004
3. Каминский А.В. Скрытое пространство-время в физике. Квантовая Магия, том 2, вып. 1 , стр. 1101-1125, 2005
4. Каминский А.В. Анатомия квантовой суперпозиции. Квантовая Магия, том 3, вып. 1, стр. 1130-1142, 2006
5. Каминский А.В. О скрытой природе спина. Квантовая Магия, том 2, вып. 2, стр. 2114-2131, 2005
6. Куракин П.В., Малинецкий Г.Г. Концепция скрытого времени и квантовая электродинамика. Квантовая Магия, том 1, вып. 2, стр. 2101-2109, 2004
7. Xiaodong Chen "A New Interpretation of Quantum Theory. Time as Hidden Variable". Department of Physics, University of Utah, Salt Lake City, UT 84112 (March 29, 2000)
8. John G. Cramer. The Transactional Interpretation of Quantum Mechanics. Reviews of Modern Physics 58, 647-688, июль 1986.
9. Колмогоров А.Н. Основные понятия теории вероятностей. М., ГНТИ, 1936.
Другие работы автора на сайте digitalphysics.ru
Каминский А.В. Этюды о неполноте // LAP Lambert Academic Publishing. 2016.