Квантовая Магия, том 9, вып. 1, стр. 1101-1136, 2012
Частицы и поля в субъективной физике
А.В. Каминский
(Получена 12 декабря 2011; опубликована 15 января 2012)
Подход, основанный на изучении реальности, порождаемой конфигурационным отношением наблюдатель - объект в замкнутом конечном мире, позволяет по-новому взглянуть на ряд не решенных концептуальных проблем физики.
Введение
Проблема наблюдателя
Наблюдатель присутствует во всех физических теориях, но, ни в одну из них он не включен явно[1]. В теории относительности, например, наблюдателя связывают с лабораторной системой координат и исследуют, как меняются с его точки зрения физические законы в других системах. В квантовой механике роль наблюдателя сводится к проецированию исследуемого квантового состояния на его, наблюдателя, приборный базис. Во всех без исключения физических теориях присутствие наблюдателя, если даже и не упоминается явно, то предполагается. И это не случайно, ибо физика, представляя собой свод законов, описывающих взаимодействие наблюдателя с окружающим миром это "теория для наблюдателя" и вне наблюдателя, она бессмысленна. Последнее входит в противоречие с парадигмальной установкой, утверждающей объективность законов природы.
Субъективная физика это научный подход в основе которого лежит понимание того факта, что все известные нам физические закономерности порождаются отношением наблюдателя (субъекта, - отсюда название) и остальной части мира. В субъективной физике физическая реальность отождествляется с пространством состояний сознания наблюдателя. Состояния сознания здесь вводятся чисто формально, как элементы некоторого множества состояний, приписываемых наблюдателю. Можно говорить о приборном базисе наблюдателя в духе квантовой механики. Теория строится формально и не предполагает отождествление субъекта с живым наблюдателем. Более того, такое отождествление приводит к противоречиям [1]. Поэтому, наблюдателя мы определяем абстрактно, как множество состояний сознания наблюдателя. Соответственно и термин "субъективность", используется исключительно, как признак отношения к наблюдателю и не имеет прямого отношения к психологии. Например, "субъективное время", наподобие "собственного времени" в теории относительности, означает время, измеряемое наблюдателем. Теория строится на строгой математической базе, поэтому, метафизические аллюзии, которые будут обнаружены философски настроенным читателем, мы оставляем на его совести.
Обратим внимание, что в отличие от разрабатываемого здесь подхода, традиционный научный метод, как раз, основан на метафизическом представлении об объективной реальности, существующей вне зависимости от наблюдателя. Не претендуя на построение законченной самосогласованной картины физической реальности, мы попытаемся ответить на вопрос - чем и в каких областях физики новый, рассматриваемый здесь взгляд может оказаться полезен? Для этого мы фрагментарно рассмотрим ряд проблем из различных областей физики и попытаемся осмыслить их с точки зрения субъективной физики.
1. Попытка аксиоматизации
Пусть S – множество осознаваемых состояний наблюдателя или, что то же самое - набор элементов физической реальности. Пусть так же H – множество состояний остальной части мира. Состояния из H не относятся к состояниям физической реальности, но составляют часть множества мировых состояний W=S ⊗ H. Субъект S конечной системы W, являющийся составной частью той же системы (S ∈ W) не может иметь полное знание о системе W. Имеет место ξ=w/s кратная вырожденность физических состояний, где w и s - мощности множеств W и S соответственно. Рассматриваемое положение вещей обозначается нами термином – "физическая (субъективная) неполнота". Геометрически, неполнота может быть описана в терминах расслоенных пространств. Мир в таком случае представляется расслоением над базовым пространством физической реальности.
Постулат 1. Физические состояния мира являются состояниями сознания.
Обратное, в общем случае, не верно. Здесь имеется в виду то, что физический мир строится над полем состояний сознания субъекта (наблюдателя). В этом смысле, физическая реальность субъективна.
Постулат 2. Множество состояний сознания Xi ∈ Subj (Subj поле сознания) конечно.
Следствие 1: Множество состояний мира W конечно.
Следствие 2: Любая траектория в пространстве состояний мира замкнута (доказательство этого утверждения тривиально). Вероятно, именно поэтому, циклические и волновые процессы так распространены в природе, а наиболее глубокая на сегодняшний день теория – квантовая механика оперирует функциональным пространством с гармоническим базисом.
Постулат 3. Отображение поля сознания Subj в себя M:|Xi>→|Xk> порождает конечные расширения поля сознания - объективный мир или его подмножества:
WR=Subj⊗Obj (1.1)
Где Obj ⊂ Subj. Это отношение удобно понимать, как субъект-объектное отношение, где в качестве объекта берется сам субъект. Будем называть его Фундаментальным субъект-объектным отношением.
Следствие: Так как порядок группы WR превосходит порядок группы Subj, то это приводит к ситуации физической неполноты [3],[4]. Неполнота ограничивает наш опыт взаимодействия и познания реальности, единственным источником которого и является это фундаментальное саморефлексивное отношение.
Состояния субъекта будем обозначать Дираковскими скобками [Subj> c левой квадратной скобкой чтобы отличить это состояние от принятого в квантовой механике (КМ), а состояния объекта двойными Дираковскими скобками ||Objj>>. Состояния [Subj> - чисто классические наблюдаемые и однозначно осознаваемые состояния. Квантовые состояния определяются тензорным произведением [Subji>||Objj>>, где i,j∈{1,2,...x} и образуют x смежных классов группы фундаментальных состояний Мира по подгруппе состояний сознания субъекта. Эти смежные классы образуют фактор группу W/Subj.
Переходы между состояниями, отображаемыми элементами группы Subj, происходят в физическом времени, тогда, как переходы между состояниями W в объективном времени. Таким образом, необходимо различать 2 шкалы времени – субъективную (физическую) и объективную. Каждый нулевой момент субъективного (или физического) времени δτ=Õ имеет длительность x единиц объективного времени. Здесь Õ - субъективный или физический ноль, в отличие от математического ноля имеет конечное значение. Неполнота выражается в ортогональности физического и объективного времени. Формально можно говорить о двумерности времени. Букву t мы далее зарезервируем для обозначения субъективного или физического времени. Будем обозначать буквой θ - объективное или алгоритмическое время. Удобно ввести еще один временной параметр – скрытое время, которое будем обозначать буквой τ. На объективном уровне имеем связь: θ=tδτ+τ, что означает, что полное время складывается из t скрытых интервалов δτ и некоторого остатка τ < δτ.
Теперь мы можем сформулировать последний постулат:
Постулат 4: Функции, определенные на поле сознания субъекта – непрерывны.
Непрерывность здесь понимается в субъективном смысле. Это означает, что изменения в системе, происходящие за время меньшее минимально осознаваемого промежутка времени δτ не должны быть замечены наблюдателем. В противном случае был бы нарушен принцип причинности, и мир был бы не структурируем.
Пусть [Xi> - состояние наблюдателя, выражаемое предикатом: "наблюдатель находится в состоянии Xi". И пусть [Xi>||Xj>> состояние, выражаемое предикатом: наблюдатель находится в состоянии Xi, а объект – в состоянии Xj. Тогда, переход [Xi>||Xj>>→[Xi+1>||Xj>>, происходящий за минимально измеримое время δτ осознаваем по определению. В то же самое время, переход [Xi>||Xj>>→[Xi>||Xj+1>>, происходящий за время меньшее минимально различимого интервала δτ не фиксируется сознанием (опять же по определению) и, соответственно, не меняет физическое состояние системы.
Если [Xi>| - координата наблюдателя, а |Xj>> - координата фотона, то Фотон при переходах [Xi>||Xj>>→[Xi>||Xj+1>> субъективно делокализован. Другими словами, с точки зрения субъекта (наблюдателя) такой фотон не может быть охарактеризован определенными координатами в пространстве.
Забегая вперед, отметим, что неполнота может быть использована не только для обоснования квантовой нелокальности, но она приводит к тому самому фундаментальному "люфту", который естественным образом обосновывает индетерминизм и необратимость на уровне физической реальности [5].
Легко понять, каким образом двумерная структура времени обосновывает квантовую нелокальность. Действительно, если физическое время не меняется, то с точки зрения двухвременного (частный случай многовременного) формализма это еще не означает, что в системе ничего не происходит. Так поведение электрона в эксперименте Юнга с точки зрения физического (субъективного) наблюдателя парадоксально - электрон проходит через две щели одновременно. На объективном уровне парадокс снимается - электрон проходит через эти щели последовательно, но за интервал времени δτ меньший субъективно различимого. Для физического наблюдателя интервал δτ строго равен нулю и поэтому для него события прохождения электрона через одну, а затем через другую щели выглядят, как одновременные.
Требование непрерывности предполагает, что за интервал времени δτ в системе может происходить все, что угодно, но в нужный момент, а именно, к окончанию скрытого интервала, все должно возвращаться в исходное (или физически бесконечно близкое) состояние, так чтобы события, происшедшие за время δτ для наблюдателя оставались не замеченными. Формально, это требование субъективной непрерывности эквивалентно топологической квазизамкнутости фазовых траекторий системы в скрытом времени.
Согласно принципу непрерывности, за минимально различимое время δτ может произойти такое же минимальное (осознанное) перемещение в пространстве, которое мы обозначим δx. Отношение величин δx и δτ должно быть универсальной константой субъективного (физического) мира. Ниже мы покажем, что эта величина равна скорости света.
Из следствия 2 постулата 2 следует замкнутость t и τ. Суммируя сказанное, можно прийти к выводу, что топология времени объективного мира представляет собой двухмерный тор T2=St ⊗ Sτ.
В отличие от Гамильтоновой динамики на торе, в нашем случае, все орбиты
замкнутые с рациональным отношением частот
![]() ,
где ni,nk ∈ N.
Из постулата непрерывности получим, как следствие, условие наблюдаемости
объекта. Оно может быть записано следующим образом:
,
где ni,nk ∈ N.
Из постулата непрерывности получим, как следствие, условие наблюдаемости
объекта. Оно может быть записано следующим образом:
![]() (1.2)
(1.2)
Аналогией является стробоскопический эффект - объект наблюдаем только в том случае, если его частота кратна частоте наблюдения. Все остальные объекты (частицы) с не кратными частотами образуют флуктуирующий вакуумный фон. Далее мы исследуем возможность обоснования квантовой механики, основываясь на перечисленных выше идеях.
2. Поле материи
Важнейшей конструкцией современной физики является, волновая функция:
ψ=A·exp(ikixi) (2.1)
отображающая точку xi вещественного пространственно-временного континуума в комплексное поле ψ. Здесь ki⊆{xα,xt} - четырёхимпульс.
Из опыта известно, что интенсивность поля P~ψψ* проявляется, как вероятность некоего дискретного осознаваемого события наблюдения. В следующем параграфе будет дано объяснение этому факту, который является одним из постулатов КМ. Отметим, что чрезвычайная эффективность КМ описания микрообъектов затмила дискомфорт непонимания его сущности и, в настоящее время, уже никто не обращает внимания на некоторую странность описания частиц полем. Полевая интерпретация волновой функции сложилась по чисто историческим причинам. До открытия КМ мы имели дело исключительно с классическими полями, волнами деформации упругой среды. Электромагнитным волнам так же приписывались механические свойства (эфир). Поэтому, после открытия волновых свойств материи, вполне естественным казалось, что функция (2.1) так же описывает распространение неких волн, подобных волнам на воде или звуковым волнам давления. И, хотя позже стало ясно, что присущая этой функции родовая комплексность таит в себе что-то совсем другое, тем не менее, полевой стереотип стал главенствующим.
Цель настоящего параграфа - раскрыть смысл волновой функции на основе, рассмотренных в предыдущем параграфе идей. Так как приведенная выше аксиоматика справедлива лишь на конечных множествах, то мы исследуем дискретный аналог волновой функции на циклической группе простого порядка:
ψ(i)=A·(αim mod l) (2.2)
l - число состояний субъекта, ψ(i)=αm - генератор группы, i - номер состояния системы, m - натуральный коэффициент, смысл которого будет выяснен позже. Множитель A временно положим A=1.
Согласно малой теореме Ферма последовательность, задаваемая геометрической прогрессией
ψ=αim mod l (2.3)
где l - простое[2], i - натуральное образует периодическую последовательность остатков (от деления на l) длиной l-1. Все эти остатки или вычеты (residue) имеют логарифмы
logα(ψ)=im (2.4)
Один и тот же вычет ψ соответствует определенному множеству значений i. То есть физические состояния образованы классами объективных состояний системы наблюдатель + объект. Логарифмы, определенные на конечных полях называют дискретными или арифметическими логарифмами. Функция ψ(i) задает отображение i→logαψ(i). Взяв дискретный логарифм ψ(i) получим точку в которую осуществляется отображение
i→im mod l (2.5)
Движение с различными m соответствуют разным импульсным состояниям
наблюдаемой, которую запишем в конечных разностях
![]() .
Обозначим их
|Pm〉=αim mod l.
Имеем
.
Обозначим их
|Pm〉=αim mod l.
Имеем
![]() (2.6)
(2.6)
Вернемся к непрерывному приближению. Рассмотрим частный (одномерный) случай волновой функции (2.1). Эта функция, заданная на непрерывном комплексном поле - полный эквивалент рассмотренной выше дискретной функции (2.2):
ψ=A·exp(ikx) (2.6)
x - здесь координата, определенная вдоль некоторой пространственной петли. Как и в прошлый раз, временно положим A=1. С точки зрения математики, поставить в соответствие вещественному числу x комплексное число ψ означает не что иное, как аналитически выполнить процесс "накатывания" фазы kx на окружность длины 2π, что, в свою очередь, означает деление числа kx на 2π (топологическая группа S1). Таким образом, подобно тому, как в дискретном аналоге ВФ над базой состояний сознания возникает слой смежных классов (группы фундаментальных состояний Мира по подгруппе состояний сознания субъекта), так и в непрерывном случае, комплексная показательная функция задает счетнолистное расслоение над комплексной плоскостью. Это подобие позволяет увидеть в ВФ физический смысл.
Предположим, что фаза ВФ (2.2), которая определяется главным значением комплексного логарифма
φ=lnψ (2.7)
играет роль скрытого параметра, определяющего исход квантово-механического измерения. Чтобы понять, как это работает, рассмотрим перемещение точки наблюдения на Δx. При этом фаза изменится на kΔx. В обычной интерпретации это просто означает, что фаза колебаний поля в точке x + Δx отлична от фазы в точке x.
Давайте теперь предположим, что никакого ψ - поля не существует, и фаза φ описывает не поле, а координату (точки в фазовом пространстве) x=Lφ/2π mod L, совершающей финитное циклическое движение. Фазовый угол 2π будет соответствовать перемещению точки отображения вдоль некоторой траектории с возвратом в исходную точку. Здесь же длина L пространственной петли вдоль которой движется частица определяется краевыми условиями задачи. Например, движение свободной частицы в пустом пространстве ограничено только размерами и топологией Вселенной. Для фотона в резонаторе краевые условия задаются положением отражающих стенок, зеркал и т.д. В любом случае, вследствие конечности Вселенной (по условию), любые подсистемы так же конечны и, соответственно, краевые условия – периодичны. Таким образом, для частицы, мы имеем отображение:
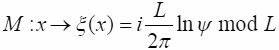 (2.8)
(2.8)
являющееся автоморфизмом на одномерной пространственной петле.
Как мы показали [6], частица в случае высших мод Lp/h>1, двигаясь в скрытом времени, "заметает" пространство вне светового конуса (пространственно подобные траектории). Поэтому, движение частицы не может быть наблюдено и воспринимается наблюдателем, как поле, существующее во всех точках некоторой области пространства одновременно. Достаточно же произвести измерение, как поле мгновенно исчезнет из всех точек пространства нелокально, ибо частица объективно не может находиться более, чем в одной точке одновременно. Этим может быть обоснована квантово-механическая R-процедура (коллапс квантового состояния). В применении к нашей модели, вероятность КМ измерения определится плотностью траекторий в субъективно нулевом объеме δV=δxδyδz пространства. Для простоты, будем рассматривать одномерный случай движения по оси x. Вероятность обнаружить частицу в области Г=xʹ<x<xʹ+δx зависит от плотности траекторий, пересекающих соответствующий элемент объема объективного пространства состояний.
Из однозначности связи между состояниями в циклической группе W, движение точки в объективном пространстве будет эргодично. Поэтому, в пределе при θ→∞ доля времени θX/θ пребывания системы в любом элементе Гx мирового объективного пространства пропорциональна объему этого элемента Δx
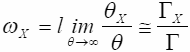 (2.9)
(2.9)
Существование этого предела (по аналогии с центральной теоремой Биркгофа — Хинчина [7] классической эргодической теории), позволяет ввести понятие вероятности. В дискретном случае это тривиально.
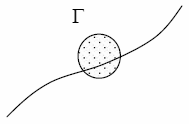
Рис.1
Мерой объема в нашем случае, является Гx=Nx - число объективных состояний, соответствующих состоянию сознания [x>.
Арнольд ввел свой особый критерий сложности числовых последовательностей и, пользуясь им, показал, что логарифм (2.4) является самой сложной функцией. «...сложность этого (дискретного авт.) логарифма, - пишет Арнольд [8], - связана с очень странным и загадочным явлением природы. Это явление встречается в разных науках под разными названиями — эргодическая теория, теория хаоса...» Это означает, что логарифмическая функция генерирует наиболее сложные (по Арнольду) последовательности чисел и, соответственно наиболее сложные орбиты в фазовом пространстве.
3. Структура субъективно расслоенных пространств и Гильбертово пространство квантовых состояний
Объективное пространство над полем мировых состояний W=S⊗H строится в ортогональном двоичном базисе с размерностью равной числу его элементов. Ортогональность обусловлена тем, что в каждый момент объективного времени мир может находиться только в одном из своих состояний. Двоичность является естественным требованием не структурируемости базовых состояний, их фундаментальности. Предположение простоты базовых состояний не снижает общности рассмотрения. Действительно, если предположить, что состояния составные, то мы всегда можем осуществить редукцию к предельному бинарному пространству большего числа измерений.
Вектор с максимальной нормой ||A||=√N=√12+12+... в таком пространстве описывает эволюцию мира во времени. Каждая проекция на базовое направление соответствует одному из состояний мира в объективном времени. Вектор с нормой ||A||<√N описывает эволюцию некоторой части мира. Так, например, вектор A={1,0,0,4,5,0,7,8}⊆Ω, где натуральными числами обозначены орты бинарного пространства, означает, что в некотором подпространстве Ω в последовательные моменты времени θ=1,4,5,7,8 реализовывались соответствующие этим номерам состояния. Нули означают, что в моменты времени θ=2,3,6 траектория системы в конфигурационном субъект – объектном пространстве находилась вне подпространства Ω.
Конфигурационное пространство W=S⊗H является расслоением над базой физического пространства состояний S. В соответствии с этим, разобьем его на кластеры физических состояний [Subj>⊂S, представляющие собой пучки векторов ||Obj>>, имеющих ненулевые проекции на базисные направления физического подпространства. На рис.2 три объективных вектора [xS>||x1>>, [xS>||x2>> и [xS>||x3>> проецируются на физическое направление |xS>. Субъект (наблюдатель), вследствие неполноты не способен отличить эти направления от направления |xS>. Поэтому, наблюдаемым параметром физического кластера может быть только скаляр, равный числу не нулевых проекций. Это вес данного физического состояния. В приведенном примере: ||A||=√NS=√12+12+12=√3.
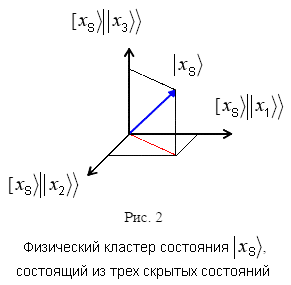
Любое физическое состояние |x1> (например, точка x на оси X пространства {XYZ}) является направлением в бинарном пространстве объективных состояний. Все точки на оси X образуют подпространство в пространстве объективных состояний. Это подпространство является конечным аналогом Гильбертова пространства физических состояний [9]. Амплитудой состояния |x> в этой конструкции является число ненулевых проекций ||A||=√Nx=√12+12+... на орты бинарного пространства объективных состояний. Если рассматривается полное мировое объективное пространство, то веса каждого из физических состояний равны ||A||=√ξ, где ξ степень субъективного вырождения. Если же рассматривается некоторая часть мира, то веса будут различны ||Ai||=√ξi (см. ниже). Теперь смысл амплитуды в выражениях для волновых функций (2.1) и (2.6) понятен. По сути, амплитуда вектора состояния является весом соответствующего состояния сознания наблюдателя.
4. Принцип суперпозиции
Как, мы уже говорили, ортогональность бинарного пространства объективных состояний является тривиальным следствием того, что система в каждый момент объективного времени может находиться только в одном состоянии (по сути само время здесь определено алгоритмически, как номер состояния). В отличие от этого, субъективно, система может находиться в нескольких состояниях одновременно. Мы уже рассмотрели эту ситуацию на примере опыта Юнга. Такое состояние называют состоянием суперпозиции [10]. Таким образом, суперпозиция – это чисто субъективное явление, обусловленное неполнотой.
Смежные классы по подгруппе состояний сознания субъекта, разделенные интервалом времени TSubj, равном времени жизни Вселенной, для наблюдателя не различимы, а это означает, что он (субъект, наблюдатель) осознает себя одновременно в x пластах времени. То есть имеет место x - кратное вырождение состояния сознания. Эта структура подобна Эвереттовскому мультиверсу, но развернута во времени. Ввиду важности этого момента для понимания квантово-механической суперпозиции, рассмотрим этот вопрос подробнее.
Фазовая траектория мира в бинарном пространстве объективных состояний замкнута, так как состояния Мира образуют конечную циклическую группу. То есть имеют место возвраты Пуанкаре. Так как мировая циклическая группа образована произведением циклических групп наблюдателя и объекта, то возвраты наблюдателя в одно из своих прежних состояний (включая память) происходят чаще, чем возвраты всей системы в свое исходное состояние. Назовем их субъективными возвратами Пуанкаре. За время одного цикла существования Вселенной TSubj реализуется ξ субъективных возвратов Пуанкаре (ξ – степень субъективного вырождения. см. выше). Субъективные возвраты осуществляются в состояния, лежащие внутри состояний сознания и, следовательно, по определению, не различимы. Очевидно, память о предыдущих посещениях этого состояния не сохраняется, ибо память о состоянии должна быть включена в определение самого состояния. Все точки возврата, разделенные субъективно-трансфинитными[3] промежутками n·TSubj, где n - натуральное, сливаются в один физический момент времени. Таким образом, "Я" наблюдателя существует одновременно в разные эпохи, сшиваемые сознанием в картину актуально существующего настоящего.
Рассмотрим структуру суперпозиции на примере с фотоном. Пусть [xi> - состояние сознания наблюдателя. Это состояние, которое может быть измерено и, следовательно, осмыслено. Например, в КМ оно может соответствовать амплитуде события обнаружения фотона в точке xi. И пусть ||xj>> - состояние, обозначающее, что фотон находится в точке с координатой xj. Это состояние мы будем называть скрытым, так как по определению оно не входит во множество осознаваемых состояний. Мировое объективное состояние записывается в виде тензорного произведения [xi>||xj>>. Эта величина является вектором в объективном пространстве состояний.
Рассмотрим физическое состояние [xi>. Ему соответствует подпространство (кластер) из ξi векторов:
[xi>||x1>>
[xi>||x2>>
... (4.1)
[xi>||xξi>>
где i=1,2,3... Субъективный наблюдатель не различает направления в этом
подпространстве и воспринимает их, как одно направление
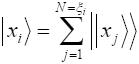 :
:
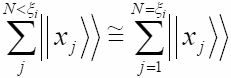 (4.2)
(4.2)
Слева - сумма любых N<ξ векторов кластера. Справа сумма всех векторов. Значок тильды над знаком равенства означает равенство в субъективном смысле.
Размерности подпространств (кластеров), относящихся к различным физическим состояниям |xi> в общем случае различны и равны ξi.
Теперь, учитывая эргодичность на объективном уровне и, следовательно,
равную долю времени пребывания системы в каждом доступном объективном
состоянии, получим, что вероятность обнаружить систему в физическом состоянии
|xi>
пропорциональна размерности соответствующего ему кластера или норме вектора.
Так как, в бинарном пространстве
![]() ,
получим:
,
получим:
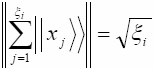 (4.3)
(4.3)
Так как различные ортогональные физические состояния |xi> могут реализоваться субъективно одновременно, то есть в пределах минимально различимого интервала времени δτ, то такое состояние воспринимается наблюдателем, как суперпозиция. В соответствии со сказанным, построим суперпозицию состояний |xi>:
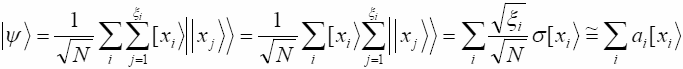 (4.4)
(4.4)
N - здесь полное число объективных состояний для всех членов суперпозиции, ξi - степени вырождения каждого члена суперпозиции. αi - нормированный весовой коэффициент. σ - единичный вектор в скрытом бинарном пространстве. Последнее равенство в субъективном смысле (см. 4.2).
5. Формализм квантовой суперпозиции
В качестве простого примера рассмотрим 8-ми мерное двоичное пространство фундаментальных состояний W. Пусть число состояний субъекта равно 2. Факторизуем это пространство W=H⊗Q, выделив двумерное пространство физических состояний H. В соответствии с этой структурой, построим вектора в W:
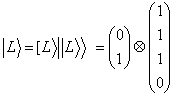 и
и
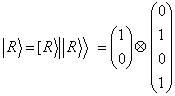 (5.1)
(5.1)
Перенумеруем все фундаментальные состояния в порядке алгоритмического времени θ. Договоримся, так же, элементы скрытого вектора располагать в порядке возрастания (сверху вниз для столбцов и слева направо для строк). Это означает следующую «зашнуровку» кластеров физических состояний L и R
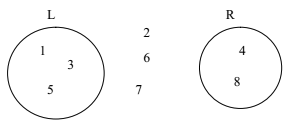
Рис.3
Состояния {2,6,7}∉{L,R}. Построим суперпозицию:
|ψ〉=[L〉||L〉〉 + [R〉||R〉〉 (5.2)
Вероятности состояний |L> и |R> легко получить, находя проекции |S> на базисные направления |L> и |R>:
![]() ;
;
![]() (5.3)
(5.3)
Чтобы найти среднее значение наблюдаемой
![]() в состоянии |ψ>,
нужно вычислить величину
в состоянии |ψ>,
нужно вычислить величину
![]() ,
где
,
где
![]() - проекционный оператор наблюдаемой.
- проекционный оператор наблюдаемой.
В объективном базисе оператор
![]() имеет вид:
имеет вид:
![]()
Проверкой получим:
![]()
Запишем оператор Ûπ/4, действующий в пространстве Subj×Obj=(2×4):
![]()
Здесь |i> - столбец из нулей с единицей на i-ом месте.
Легко видеть, что квадрат оператора Ûπ=(Ûπ/4)2 определяет операцию √NOT, переводящую базисное состояние в состояние суперпозиции. Оператор Ûπ=(Ûπ/4)4 инвертирует состояния (NOT).
6. Проблема фазы
В квантовой теории существует не доказанное правило (тезис), согласно которому, любой измеримой величине сопоставляется эрмитовый оператор. Этот тезис побуждает искать эрмитовый оператор фазы. Однако, доказано, что в Гильбертовом пространстве такого оператора не существует.
Эта проблема до сих пор не понята до конца. В свете излагаемой здесь концепции, фаза – скрытый параметр и ей нельзя сопоставить ни какую наблюдаемую по сути.
Так как операторы рождения и уничтожения вводятся через квадратурные компоненты
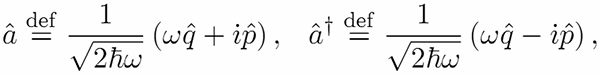 (6.6)
(6.6)
естественным кажется представить их по формуле Эйлера, введя, тем самым оператор фазы:
![]() (6.7)
(6.7)
Где
![]() и
и
![]() предполагаются эрмитовыми:
предполагаются эрмитовыми:
![]() ,
,
![]() (6.8)
(6.8)
Поэтому
![]() (6.9)
(6.9)
В результате имеем:
![]() (6.10)
(6.10)
![]() (6.11)
(6.11)
Где операторы рождения и уничтожения имеют вид:

 (6.12)
(6.12)
Соответственно, экспоненциальные операторы фазы имеют вид:
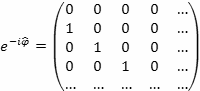
 (6.13)
(6.13)
Казалось бы все в порядке, - мы имеем экспоненциальный оператор фазы
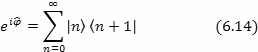
Спектр собственных векторов которого:
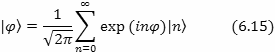
Эти векторы известны, как фазовые состояния Сусскинда-Глоговера. Из последнего соотношения следует, что если фаза рассматривается, как наблюдаемая, сопряженная числу квантов, то при фиксированной фазе число квантов полностью не определено, как это имеет место для когерентного света.
Однако, проблема в том, что векторы
![]() не ортогональны (базис переполнен), оператор (6.24) не ортогонален и
соответственно оператор
не ортогональны (базис переполнен), оператор (6.24) не ортогонален и
соответственно оператор
![]() не эрмитов[4].
Этот факт, не замеченный Дираком, впервые отметил Лондон [11].
не эрмитов[4].
Этот факт, не замеченный Дираком, впервые отметил Лондон [11].
Неортогональность
![]() связана с односторонностью спектра оператора (6.25).
связана с односторонностью спектра оператора (6.25).
Существует 2 способа решения этой проблемы. Либо ввести отрицательные числа заполнения, либо рассматривать конечные пространства состояний. Очевидно, что первый способ физически не релевантен. Второй же метод, примененный Пеггом и Барнеттом [12]представляет для нас большой интерес. И, хотя, обращение к конечному аналогу Гильбертова пространства может рассматриваться, как формальный прием, мы считаем его физически обоснованным (см. выше).
По аналогии с (5.5) рассмотрим оператор :
![]() (6.16)
(6.16)
Здесь и далее мы пользуемся общепринятой нотацией Фоковских состояний. В матричном представлении он имеет вид:

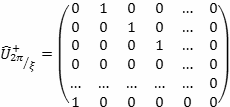 (6.17)
(6.17)
Действие оператора
![]() на Фоковские состояния тривиально:
на Фоковские состояния тривиально:
![]() (6.18)
(6.18)
![]()
Оператор
![]() являясь генератором циклической группы
ξ
-го порядка, может быть использован для описания осциллятора.
n-кратное применение оператора
являясь генератором циклической группы
ξ
-го порядка, может быть использован для описания осциллятора.
n-кратное применение оператора
![]() к вектору
|i>
возвращает его в исходное состояние. Рекуррентное уравнение
к вектору
|i>
возвращает его в исходное состояние. Рекуррентное уравнение
![]() (6.19)
(6.19)
Описывает движение по замкнутой орбите в фазовом пространстве состояний.
Естественно, для описания осциллятора, использовать конечные поля Галуа GF(np). Здесь p – простое, n – натуральное числа.
Рассмотрим в качестве простого примера поле GF(23).
Примитивными полиномами, которого являются
![]() (11) и
(11) и
![]() (13). В скобках указывается двоично-десятичная нотация.
(13). В скобках указывается двоично-десятичная нотация.
Элемент поля
![]() является порождающим. То есть он является корнем 8 степени из единицы поля.
Соответственно, степени этого элемента покрывают все поле.
Воспользуемся нумерацией, возникающей в порядке порождения:
является порождающим. То есть он является корнем 8 степени из единицы поля.
Соответственно, степени этого элемента покрывают все поле.
Воспользуемся нумерацией, возникающей в порядке порождения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() (6.20)
(6.20)
Назовем номера элементов – фазой.
Теперь динамику осциллятора мы можем описать двумя эквивалентными способами – уравнением (6.7) или же аналогичным уравнением:
![]() (6.21)
(6.21)
Где
![]() - порождающий элемент (генератор группы).
- порождающий элемент (генератор группы).
Пусть вектор
![]() описывает пространственное распределение частиц в моде. Если в моде
описывает пространственное распределение частиц в моде. Если в моде
![]() состояний, то число частиц в моде
состояний, то число частиц в моде
![]() .
Кроме этого, ни какие 2 частицы не могут разделять одно и то же объективное
состояние
.
Кроме этого, ни какие 2 частицы не могут разделять одно и то же объективное
состояние
![]() .
Движение в моде может иметь произвольную фазу от 0 до
.
Движение в моде может иметь произвольную фазу от 0 до
![]() ,
отсчитываемую от некоторого условного нулевого значения, например от
,
отсчитываемую от некоторого условного нулевого значения, например от
![]() .
.
Фурье образ вектора
![]()
![]() (6.22)
(6.22)
частотный пространственный спектр распределения частиц
![]() .
Где
.
Где
![]() – матрица преобразования Фурье над полем Галуа. По сути
– матрица преобразования Фурье над полем Галуа. По сути
![]() Состояние Фока или состояние в котором число частиц в моде равно n.
Обратное преобразование дает полный ортонормированный набор фазовых векторов:
Состояние Фока или состояние в котором число частиц в моде равно n.
Обратное преобразование дает полный ортонормированный набор фазовых векторов:
![]()
Унитарная матрица
![]() является изоморфным аналогом дискретного преобразования Фурье в методе Пегга и
Барнетта (см. ниже).
является изоморфным аналогом дискретного преобразования Фурье в методе Пегга и
Барнетта (см. ниже).
Матрица преобразования
![]() имеет вид.
имеет вид.
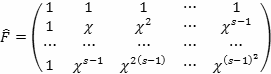 (6.24)
(6.24)
Где
![]() - примитивный корень
ξ
-ой степени из 1.
- примитивный корень
ξ
-ой степени из 1.
Номер компоненты базисного вектора
![]() отличной от нуля дает число частиц в моде, а сама компонента – фазу движения
частиц в моде.
отличной от нуля дает число частиц в моде, а сама компонента – фазу движения
частиц в моде.
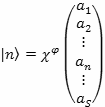 (6.25)
(6.25)
Где
![]() кроме
кроме
![]() ;
;
![]() .
Фазовый множитель
.
Фазовый множитель
![]() мы вынесли, как скаляр.
мы вынесли, как скаляр.
Рассмотрим действие оператора (6.16) на вектор
![]() над полем Галуа с числом элементов
над полем Галуа с числом элементов
![]() .
.
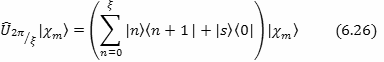
Учитывая (6.22) и (6.24) имеем
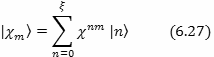
Подставляя в (6.26) и перемножая суммы, а так же учитывая, что
![]() ,
после не сложных преобразований, получим уравнение на собственные значения:
,
после не сложных преобразований, получим уравнение на собственные значения:
![]()
То есть, действие оператора
![]() в своем собственном представлении на фазовый вектор сводится к умножению на
в своем собственном представлении на фазовый вектор сводится к умножению на
![]() то есть, сдвигу фазы (см. 6.9).
то есть, сдвигу фазы (см. 6.9).
Таким образом, вместо экспоненциального оператора фазы, введенного Дираком и оказавшемся не унитарным:
![]()
мы ввели унитарный оператор
![]() действующий на конечном поле Галуа.
действующий на конечном поле Галуа.
![]()
Это позволяет построить эрмитовый оператор фазы:
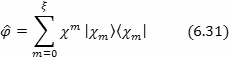
Проблема фазы показывает нам, что традиционный подход к квантовой механике имеет ограничения, которые естественным образом решаются при переходе к конечным полям.
7. Импульс и энергия
Импульс, как и в обычной механике, определяется, как интегральный инвариант относительно трансляций в пространстве (здесь на циклической группе):
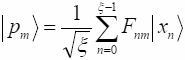 (7.1)
(7.1)
m- порядок моды или, другими словами, число прыжков на замкнутой орбите.
![]() - матрица (6.24),
- матрица (6.24),
![]() - элементы циклической группы.
Суммирование идет по конечному множеству вырожденных состояний (Эвереттовских
миров). Аналогично, частота или энергия определяются, как инвариант по
времени. То есть это некое состояние не меняющееся при трансляции во времени.
- элементы циклической группы.
Суммирование идет по конечному множеству вырожденных состояний (Эвереттовских
миров). Аналогично, частота или энергия определяются, как инвариант по
времени. То есть это некое состояние не меняющееся при трансляции во времени.
Инвариантность суперпозиции (7.1) легко видеть на частном примере, где
![]() =1. Легко видеть, что воздействуя на правую часть (7.1) оператором эволюции
=1. Легко видеть, что воздействуя на правую часть (7.1) оператором эволюции
![]() выражение (7.1) переходит само в себя. Если же все коэффициенты различны,
то воздействие оператора эволюции сводится только к появлению добавочного
фазового множителя, перемещающего наблюдателя между эвереттовскими эпохами,
но оставляя в пределах физического состояния.
выражение (7.1) переходит само в себя. Если же все коэффициенты различны,
то воздействие оператора эволюции сводится только к появлению добавочного
фазового множителя, перемещающего наблюдателя между эвереттовскими эпохами,
но оставляя в пределах физического состояния.
Существование состояний
![]() и
и
![]() ,
инвариантных по соответствующим сопряженным переменным x и t,
как известно, свидетельствует об определенных симметриях физического
4-х мерного многообразия, из которых, согласно теореме Нетер,
вытекают законы сохранения.
,
инвариантных по соответствующим сопряженным переменным x и t,
как известно, свидетельствует об определенных симметриях физического
4-х мерного многообразия, из которых, согласно теореме Нетер,
вытекают законы сохранения.
В непрерывном приближении, удобно перейти к комплексному полю
и рассматривать разложение на дискретном базисе Фурье. Тогда оператор
![]() следует заменить оператором:
следует заменить оператором:
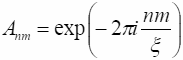 (7.2)
(7.2)
Дискретный аналог ВФ примет вид:
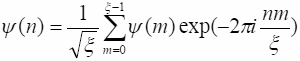 (7.3)
(7.3)
здесь
![]() ;
;
Чтобы перейти к привычной форме записи волновой функции, преобразуем аргумент под экспонентой (7.3):
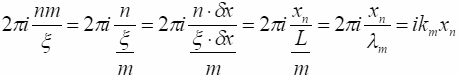 (7.4)
(7.4)
Здесь мы воспользовались тем, что:
![]() ;
;
![]() и обозначили
и обозначили
![]() .
(7.5)
.
(7.5)
Здесь
δx
- элементарная, различимая субъектом (в данной экспериментальной конфигурации)
длина;
![]() - число пропусков состояний при движении, L - длина пространственной петли,
вдоль которой рассматривается движение. l - "длина волны".
- число пропусков состояний при движении, L - длина пространственной петли,
вдоль которой рассматривается движение. l - "длина волны".
В итоге получим:
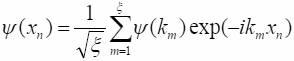 (7.6)
(7.6)
Аналогично:
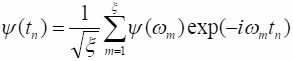 (7.7)
(7.7)
Устремив
![]() ;
;
![]()
![]() [5]
и заменяя суммы интегралами, можно перейти к непрерывным выражениям,
осуществляющим переход между импульсным и координатным представлениями,
а так же временным и частотным, которые мы здесь выписывать не будем.
[5]
и заменяя суммы интегралами, можно перейти к непрерывным выражениям,
осуществляющим переход между импульсным и координатным представлениями,
а так же временным и частотным, которые мы здесь выписывать не будем.
Из (7.6), (7.7) следуют соотношения неопределённостей:
![]() (7.10)
(7.10)
Функция
![]() определяет распределение частиц в пространстве (здесь в одном измерении).
В общем случае мы должны рассмотреть пакет частиц, движущихся
по пространственно-подобным орбитам (аналог волнового пакета):
определяет распределение частиц в пространстве (здесь в одном измерении).
В общем случае мы должны рассмотреть пакет частиц, движущихся
по пространственно-подобным орбитам (аналог волнового пакета):
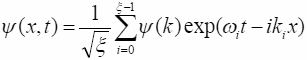 (7.11)
(7.11)
С точки зрения физического наблюдателя все ξ Эвереттовских миров независимы, так как неполнота не позволяет ему видеть их связь. Каждая частица здесь – Эвереттовский экземпляр. (В параграфе 6 мы рассматривали многочастичные системы, где в i-ом эвереттовском мире находилось ni частиц).
8. Объективная скорость
Рассмотрим простейший пример одномерного движения в непрерывном приближении.
Как мы говорили выше, состояние системы может быть записано в виде
![]() .
Или в виде функции
.
Или в виде функции
![]() описывающей отображение:
описывающей отображение:
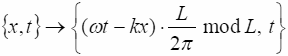 .
(8.1)
.
(8.1)
Обозначим:
![]() (8.2)
(8.2)
Здесь
![]() - координата точки (фотона) относительно наблюдателя, а
- координата точки (фотона) относительно наблюдателя, а
![]() - координата самого наблюдателя. Объективную скорость частицы получим, взяв
производную по времени от (8.2). Учитывая, что L=ln, а так же то, что
- координата самого наблюдателя. Объективную скорость частицы получим, взяв
производную по времени от (8.2). Учитывая, что L=ln, а так же то, что
![]() ,
получим:
,
получим:
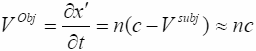 (8.3)
(8.3)
То есть объективная скорость принимает кратные
![]() значения хотя, как легко видеть, подчиняется обычному закону сложения скоростей.
значения хотя, как легко видеть, подчиняется обычному закону сложения скоростей.
9. Субъективная скорость
Вычислим субъективную скорость точки для k-ой моды (компоненты суперпозиции) (скорость фотона относительно наблюдателя). Ее можно определить, записав условие встречи точки (фотона) с наблюдателем [6]:
![]() ;
из (8.2) получим:
;
из (8.2) получим:
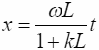 ;
то есть
;
то есть
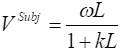 ;
(9.1)
;
(9.1)
Для мод высокого порядка
(![]() ),
получим
),
получим
![]() .
.
Учитывая, что
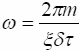 ;
;
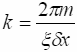 ;
соответственно, получим:
;
соответственно, получим:
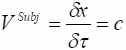 (9.2)
(9.2)
Этот простой пример показывает, что:
Скорость точки встречи наблюдателя с фотоном (субъективная скорость света) является универсальной константой, не зависящей от скорости наблюдателя.
Не трудно понять, что полученная независимость скорости света от скорости наблюдателя (аксиома СТО), является следствием субъект-объектной "зацепленности" фотона с наблюдателем. Ниже мы вернемся к этому вопросу.
Следует заметить, что любое физическое событие означает выполнение "условия встречи" (оно же условие наблюдаемости (1.2)) состояний в зацепленных группах:
![]()
Это Диофантово уравнение "зацепляет" группы субъекта и объекта
по параметру θ. Решив это уравнение мы могли бы определить
фундаментальное "время" θ, а с ним и физическое время
![]() наступления заданного события, но это принципиально не возможно вследствие
физической неполноты, формально выражающейся, как U(1) симметрия и, скрывающей
от субъекта относительную фазу зацепления циклических групп. Единственное,
что нам доступно, это определить вероятность данного события.
наступления заданного события, но это принципиально не возможно вследствие
физической неполноты, формально выражающейся, как U(1) симметрия и, скрывающей
от субъекта относительную фазу зацепления циклических групп. Единственное,
что нам доступно, это определить вероятность данного события.
Множество точек пересечения мировых линий фотона и наблюдателя дается
последовательностью отображений Пуанкаре [7]:
![]() в пространстве
в пространстве
![]() .
Множество этих точек лежит на гиперповерхности
.
Множество этих точек лежит на гиперповерхности
![]() светового конуса.
светового конуса.
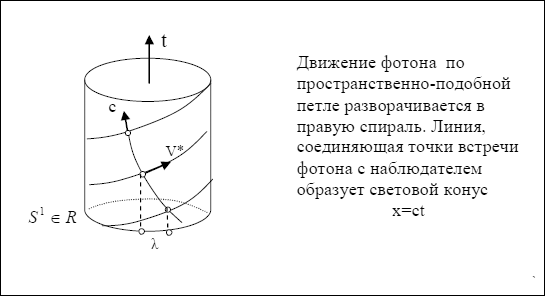
Рис.4
Отображение Пуанкаре связывает дискретную динамику с непрерывной [13],
описываемой дифференциальными уравнениями и используется, как формальный метод,
упрощающий исследования квазипериодической Гамильтоновой динамики. В этой
математической структуре просматривается нечто большее, чем вычислительный
прием, - отображение Пуанкаре описывает редукцию от фундаментальной
детерминированной механики к субъективной физике. При этом, траектория фотона
![]() ,
генерируемая отображением Пуанкаре, предстает для наблюдателя дискретным
множеством точек (пунктиром). Расстояние между точками, при этом, равно длине
волны. Наблюдателю кажется, что фотон движется по образующей светового конуса
со скоростью c, так как реальное сверхсветовое движение находится вне его
восприятия. При переходе к модам n более высокого порядка, витки спирали
на рисунке сближаются как
,
генерируемая отображением Пуанкаре, предстает для наблюдателя дискретным
множеством точек (пунктиром). Расстояние между точками, при этом, равно длине
волны. Наблюдателю кажется, что фотон движется по образующей светового конуса
со скоростью c, так как реальное сверхсветовое движение находится вне его
восприятия. При переходе к модам n более высокого порядка, витки спирали
на рисунке сближаются как
![]() ,
а длина волны так же уменьшается, как
,
а длина волны так же уменьшается, как
![]() ,
так, что субъективная скорость остается равной с.
,
так, что субъективная скорость остается равной с.
10. Картина Калуцы – Клейна [14] и калибровочные симметрии в контексте модели субъективной физики. Масса, заряд, действие
Обычная волновая функция описывает движение в скрытом времени. Но неполнота предполагает существование также и скрытого пространства. В этом параграфе мы рассмотрим наиболее общий случай движения с участием скрытых пространственных степеней свободы.
Для ЭМ-поля
![]() ,
где n-номер моды. При
,
где n-номер моды. При
![]()
![]() объективная скорость (8.3) примет максимально возможное значение
объективная скорость (8.3) примет максимально возможное значение
![]() .
Для свободного поля (в отличие от поля в резонаторе длиной L), максимальная
скорость фотона является еще одной универсальной константой с размерностью
скорости, и большей скорости света в L/dx раз. Где L - линейный размер
Вселенной, а dx – "квант" длины. Длина волны при этом
.
Для свободного поля (в отличие от поля в резонаторе длиной L), максимальная
скорость фотона является еще одной универсальной константой с размерностью
скорости, и большей скорости света в L/dx раз. Где L - линейный размер
Вселенной, а dx – "квант" длины. Длина волны при этом
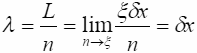 (10.1)
(10.1)
Это минимальная длина волны для ЭМ поля.
Для n>x длина волны становится меньше минимально различимой наблюдателем
величины dx. Это возможно, так как
![]() ,
но не
,
но не
![]() .
Формально это означает, что частица теперь движется не только в протяженном
измерении x, но и в ортогональном компактифицированном измерении
с периметром δx. Эту степень свободы будем обозначать
.
Формально это означает, что частица теперь движется не только в протяженном
измерении x, но и в ортогональном компактифицированном измерении
с периметром δx. Эту степень свободы будем обозначать
![]() - скрытая координата. Когда длина волны света становится меньше характерного
размера dx, возбуждается компактифицированная мода колебаний рис.5.
- скрытая координата. Когда длина волны света становится меньше характерного
размера dx, возбуждается компактифицированная мода колебаний рис.5.
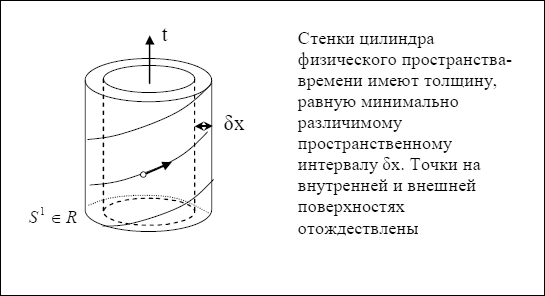
Рис.5
Продольная (вдоль большого круга) мода связана с энергией движения, тогда, как – поперечная (вдоль компактифицированного измерения dx) обязана энергии, формирующей массу и заряд. Масса это энергия покоящегося тела. Этому факту в теории относительности отвечает формула Е0=тс2, где Е0 – энергия покоя. По сути, формула Эйнштейна является определением массы.
Ниже мы рассмотрим движение по многообразию с тривиальным расслоением,
генерирующее бозе-подобные массивные поля. Таких полей в природе не
наблюдается по той причине, что реальное расслоение не тривиально. Однако, мы
здесь ограничимся этим более простым случаем, не снижающим уровень понимания
проблемы. Рассмотрим поле траекторий
![]() на объективном многообразии с метрикой
на объективном многообразии с метрикой
![]() (10.2)
(10.2)
![]() .
Псевдоевклидовость метрики принципиально не влияет на следующие выводы.
А ниже, в следующем параграфе мы обсудим происхождение такой метрики.
Воспользовавшись цикличностью скрытой координаты
.
Псевдоевклидовость метрики принципиально не влияет на следующие выводы.
А ниже, в следующем параграфе мы обсудим происхождение такой метрики.
Воспользовавшись цикличностью скрытой координаты
![]() ,
разложим его в ряд Фурье по модам в xh
,
разложим его в ряд Фурье по модам в xh
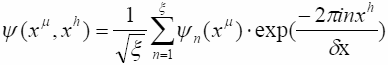 (10.3)
(10.3)
![]() (10.4)
(10.4)
Здесь
![]() - скрытая (поперечная) координата,
δx
- периметр по
- скрытая (поперечная) координата,
δx
- периметр по
![]() ,
n – номер поперечной моды,
,
n – номер поперечной моды,
![]() - 4-х импульс n-ой гармоники. Сначала рассмотрим одну n-ю гармонику поля (10.3)
- 4-х импульс n-ой гармоники. Сначала рассмотрим одну n-ю гармонику поля (10.3)
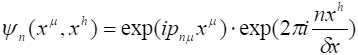
Подставляя это решение в пятимерное "волновое" уравнение:
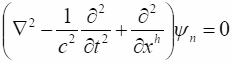 ,
(10.3)
,
(10.3)
Заключив слово "волновое" в кавычки, мы напоминаем читателю, что в данном случае это уравнение описывает траектории безмассовых частиц. Получим характеристическое уравнение дисперсии для массивных частиц:
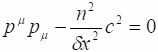 ,
,
В трехмерном виде:
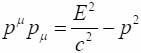 ,
и в результате
,
и в результате
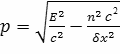 (10.4)
(10.4)
Таким образом, роль массы выполняет величина
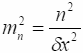
Итак, масса определяется номером моды n при движении безмассовой частицы (фотона) в скрытом измерении и масштабом компактификации.
Если
![]() ,
то четырёхимпульс имеет нулевой модуль, что соответствует безмассовым фотонам.
,
то четырёхимпульс имеет нулевой модуль, что соответствует безмассовым фотонам.
Принципиальным для дальнейшего рассмотрения моментом является независимость
протяженных (наблюдаемых) степеней свободы
![]() от скрытой степени свободы
от скрытой степени свободы
![]() .
Это условие, известное, как условие цилиндричности, чисто формально
использовалось в ранних многомерных теориях. Цилиндричность
является аналитическим выражением субъективной неполноты мира.
Она означает независимость состояний сознания наблюдателя от скрытых состояний.
.
Это условие, известное, как условие цилиндричности, чисто формально
использовалось в ранних многомерных теориях. Цилиндричность
является аналитическим выражением субъективной неполноты мира.
Она означает независимость состояний сознания наблюдателя от скрытых состояний.
Рассмотрим общие преобразования координат в объективном пространстве:
![]() (10.4)
(10.4)
Распишем по компонентам:
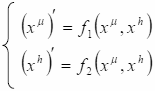 (10.5)
(10.5)
При наложении условия цилиндричности
![]() преобразования (10.5) сужаются до:
преобразования (10.5) сужаются до:
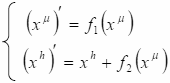 (10.6)
(10.6)
Здесь для наглядности записи мы использовали индексы: μ – subj и h – hide, пробегающие значения 0,1,2,3 и 4 соответственно. Вычислим компоненты Gμh метрического тензора Gik. С учетом условия независимости физических координат от скрытой координаты xh, получим:
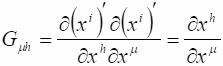 (10.7)
(10.7)
Возьмем производную по
![]() от второго уравнения (10.6)
от второго уравнения (10.6)
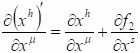 ;
Отождествляя Gμh с вектор потенциалом
Αμ,
получим градиентную инвариантность (калибровочное преобразование)
для электромагнитного поля:
;
Отождествляя Gμh с вектор потенциалом
Αμ,
получим градиентную инвариантность (калибровочное преобразование)
для электромагнитного поля:
![]() .
Отсюда можно сделать вывод, что калибровочная структура теории, навязывается
тем же самым принципом субъективной неполноты, приводящим к существованию
скрытого измерения
xh.
.
Отсюда можно сделать вывод, что калибровочная структура теории, навязывается
тем же самым принципом субъективной неполноты, приводящим к существованию
скрытого измерения
xh.
Теперь посмотрим, как преобразуется поле ψ при калибровочном преобразовании.
Поле (10.2) при преобразовании скрытых координат
![]() преобразуется следующим образом:
преобразуется следующим образом:
![]() (10.8)
(10.8)
Сравним правую и левую части равенства:
![]()
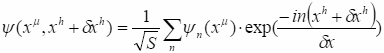
Получим:
![]() (10.9)
(10.9)
Где
![]() .
Именно так преобразуются заряженные скалярные поля при калибровочных
преобразованиях. Это означает, что редуцированная к физическому
пространству-времени фурье компонента
.
Именно так преобразуются заряженные скалярные поля при калибровочных
преобразованиях. Это означает, что редуцированная к физическому
пространству-времени фурье компонента
![]() пятимерного поля
пятимерного поля
![]() воспринимается субъектом, как заряженное скалярное поле с зарядом
воспринимается субъектом, как заряженное скалярное поле с зарядом
![]() .
.
Заметим, что величина
![]() является действием и значит
является действием и значит
![]() часть плотности лагранжиана, отвечающая за взаимодействие поля с зарядом.
Действие
часть плотности лагранжиана, отвечающая за взаимодействие поля с зарядом.
Действие
![]() - число витков по скрытой координате.
- число витков по скрытой координате.
Перепишем (10.4) в виде:
![]() (10.11)
(10.11)
Здесь
![]() - скрытый волновой вектор. Случай
- скрытый волновой вектор. Случай
![]() соответствует отсутствию дисперсии
соответствует отсутствию дисперсии
![]() .
При
.
При
![]() мы имеем дисперсию в вакууме, как для массивных частиц. Наличие дисперсии для
тяжелых частиц обусловлено движением в скрытом пространстве (Внутри стенки
цилиндра рис.5). Групповая скорость равна:
мы имеем дисперсию в вакууме, как для массивных частиц. Наличие дисперсии для
тяжелых частиц обусловлено движением в скрытом пространстве (Внутри стенки
цилиндра рис.5). Групповая скорость равна:
![]() ,
откуда
,
откуда
![]() (10.12)
(10.12)
подставляя
![]() из (10.12) обратно в (10.11) и учитывая, что
из (10.12) обратно в (10.11) и учитывая, что
![]() ,
где n - порядок поперечной моды, после не сложных преобразований, получим:
,
где n - порядок поперечной моды, после не сложных преобразований, получим:
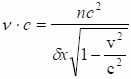 (10.13)
(10.13)
Учитывая,
![]() ,
перепишем (10.13) в естественной системе единиц. Для случая
,
перепишем (10.13) в естественной системе единиц. Для случая
![]() получим:
получим:
![]() (10.14)
(10.14)
Напомним, что
![]() и
и
![]() .
Это выражение в обычной метрической системе соответствует:
.
Это выражение в обычной метрической системе соответствует:
![]() .
Учитывая, что
.
Учитывая, что
![]() или, что то же самое
или, что то же самое
![]() ,
мы видим, что масса в покое равна числу длин волн в компактифицированной моде
или, что то же самое, числу колебаний, совершаемых фотоном за субъективно
нулевой момент времени
δτ.
То есть массу можно интерпретировать, как скрытую энергию. Таким образом,
субъективная неполнота приводит к калибровочной
,
мы видим, что масса в покое равна числу длин волн в компактифицированной моде
или, что то же самое, числу колебаний, совершаемых фотоном за субъективно
нулевой момент времени
δτ.
То есть массу можно интерпретировать, как скрытую энергию. Таким образом,
субъективная неполнота приводит к калибровочной
![]() симметрии по теореме Нетер соответствующей компенсирующим калибровочным полям
Αμ
и взаимодействующим с ними массивными заряженными полями с массами
симметрии по теореме Нетер соответствующей компенсирующим калибровочным полям
Αμ
и взаимодействующим с ними массивными заряженными полями с массами
![]()
Свойства симметрий этих степеней свободы обусловливает ряд законов сохранения различных квантовых чисел. Законы сохранения зарядов связаны с симметриями скрытых (субъективно-скрытых) компактифицированных измерений.
Мы показали, что калибровочные симметрии на которых строится Стандартная
Модель связаны с циклической группой
![]() классов эквивалентности по подгруппе состояний сознания. Эта структура
накладывает определенные ограничения на возможную топологию и геометрию
субъективного пространства.
классов эквивалентности по подгруппе состояний сознания. Эта структура
накладывает определенные ограничения на возможную топологию и геометрию
субъективного пространства.
11. Топология и геометрия субъективного метрического пространства
Фундаментальное Субъект-объектное отношение
WR=Subj⊗Obj
генерирует проективное пространство состояний наблюдателя. Это следует из того,
что единственным способом объединения групп субъекта и объекта является прямое
произведение
![]() ,
когда преобразования соответствующих симметрии действуют независимо.
Существует теорема Райферти [15], лимитирующая объединение внутренних и
пространственно-временных симметрий. Согласно этой теореме, нет физически
удовлетворительного способа объединить группы Ли (Obj) конечного ранга,
относящиеся к внутренним симметриям, и группу Пуанкаре (Subj)
пространственно-временной симметрии. Как мы видим, смысл этой теоремы
в субъективной физике очевиден. Кроме этого, субъективная физика позволяет
детализировать характер самого расслоения
WR=Subj⊗Obj.
Вспомним, что каждое состояние субъекта является классом эквивалентности по
"фазе" циклического поля скрытых состояний. Но пространство классов
эквивалентности это проективное пространство[6].
Мы пришли к важному выводу: физическое пространство - проективно.
,
когда преобразования соответствующих симметрии действуют независимо.
Существует теорема Райферти [15], лимитирующая объединение внутренних и
пространственно-временных симметрий. Согласно этой теореме, нет физически
удовлетворительного способа объединить группы Ли (Obj) конечного ранга,
относящиеся к внутренним симметриям, и группу Пуанкаре (Subj)
пространственно-временной симметрии. Как мы видим, смысл этой теоремы
в субъективной физике очевиден. Кроме этого, субъективная физика позволяет
детализировать характер самого расслоения
WR=Subj⊗Obj.
Вспомним, что каждое состояние субъекта является классом эквивалентности по
"фазе" циклического поля скрытых состояний. Но пространство классов
эквивалентности это проективное пространство[6].
Мы пришли к важному выводу: физическое пространство - проективно.
Вспомогательное пространство однородных координат, которое, обычно, вводят
формально при рассмотрении проективной геометрии, здесь приобретает реальный
смысл объективного пространства, где добавочная 5-я координата
![]() является скрытой координатой, обусловленной субъективной физической неполнотой.
Формально, псевдоевклидовость метрики физического мира обусловлена выбором
абсолюта (11.1). Покажем, что этот особый характер метрики так же индуцируется
субъективным характером наблюдателя.
является скрытой координатой, обусловленной субъективной физической неполнотой.
Формально, псевдоевклидовость метрики физического мира обусловлена выбором
абсолюта (11.1). Покажем, что этот особый характер метрики так же индуцируется
субъективным характером наблюдателя.
Так как пространство
![]() фундаментально, то оно действительное. Если бы оно было хотя бы частично
комплексно, то это означало бы добавочную степень свободы. Это исключает
положительно определенные сигнатуры квадратичных форм
фундаментально, то оно действительное. Если бы оно было хотя бы частично
комплексно, то это означало бы добавочную степень свободы. Это исключает
положительно определенные сигнатуры квадратичных форм
![]() .
Так форма:
.
Так форма:
![]()
Не имеет ни какого физического смысла, ибо не соответствует ни какому действительному многообразию.
Поэтому, выбор остается между формами:
![]()
![]()
Так как
![]() одной природы, то они должны иметь одинаковый знак. Заметим, что обе формы,
рассматриваемые, как абсолюты инвариантны относительно группы преобразований,
соответствующих псевдоевклидовой геометрии. Этим мы доказали, что физическое
проективное пространство-время неизбежно псевдоевклидово. Вопрос выбора между
формами (11.2) и (11.3) это вопрос интерпретации. Известно, что преобразования
однородных координат
одной природы, то они должны иметь одинаковый знак. Заметим, что обе формы,
рассматриваемые, как абсолюты инвариантны относительно группы преобразований,
соответствующих псевдоевклидовой геометрии. Этим мы доказали, что физическое
проективное пространство-время неизбежно псевдоевклидово. Вопрос выбора между
формами (11.2) и (11.3) это вопрос интерпретации. Известно, что преобразования
однородных координат
![]() ,
сохраняющие (11.2) при переходе к неоднородным координатам
,
сохраняющие (11.2) при переходе к неоднородным координатам
![]() ;
;
![]() образуют группу преобразований Лоренца [16], оставляющую инвариантным интервал:
образуют группу преобразований Лоренца [16], оставляющую инвариантным интервал:
![]()
Именно так - как теория субъективного наблюдателя, и возникает специальная теория относительности. Еще раз подчеркнем - псевдоевклидовость метрики физического пространства-времени это следствие субъективно конфигурационного отношения наблюдатель - мир. Мы без ущерба можем перейти к другой - объективной точке зрения. Переписав (11.4) в виде:
![]()
Будем считать время мероопределением в некоем пространстве координат
и действия
![]() .
.
Чтобы получить уравнения движения, обычно варьируют действие в выражении (11.4). Но с тем же успехом мы можем варьировать время в выражении (11.5). И в одном и в другом случае, мы получим одни и те же уравнения. В [4] мы показали, что принцип наименьшего времени для объективного наблюдателя заменяет принцип наименьшего действия, который является принципом субъективного наблюдателя.
Теперь, зная, что физическое пространство проективно, компактно и
периодично по своим координатам, мы можем сконструировать его из 4-х мерного
тора
![]() ,
путем сшивки по классам эквивалентности (прямым в R5)
его антиподальных точек. В результате получим 4-х мерную бутылку Клейна.
Известно, что любое проективное пространство RP(n) четной размерности n
является неориентируемым [17]. Поэтому, 4-х бутылка тоже неориентируема.
Ниже будет показано, что существование в природе фермионов (Группа SU(2))
служит прямым свидетельством неориентируемости физического многообразия
,
путем сшивки по классам эквивалентности (прямым в R5)
его антиподальных точек. В результате получим 4-х мерную бутылку Клейна.
Известно, что любое проективное пространство RP(n) четной размерности n
является неориентируемым [17]. Поэтому, 4-х бутылка тоже неориентируема.
Ниже будет показано, что существование в природе фермионов (Группа SU(2))
служит прямым свидетельством неориентируемости физического многообразия
![]() .
Остается, однако не ясной возможность существования лагранжиана на таком
многообразии.
.
Остается, однако не ясной возможность существования лагранжиана на таком
многообразии.
Тождественность частиц и принцип Паули
Принцип Паули утверждает, что волновая функция системы фермионов антисимметрична относительно перестановки любых двух из них. В рамках квантовой релятивистской теории поля доказывается теорема о связи спина со статистикой. Теорема увязывает спин частиц с поведением ВФ относительно перестановок частиц. Доказательство весьма сложно и использует большое количество допущений. Кроме всего прочего, теорема не отвечает на главный вопрос - почему в природе все частицы делятся на 2 сорта - бозоны, подчиняющиеся тензорной алгебре и фермионы, подчиняющиеся спинорной алгебре. Как показали Фейнман и John Baez, имеет место простая физическая интерпретация этой теоремы [18],[19], основанная на понимании топологической природы спина. Мы воспользуемся тем же методом и рассмотрим движение скалярных частиц (фотонов) в пространстве с субъективно - индуцированной топологией. Как мы показали выше, 4-х мерное физическое многообразие наблюдателя является 4-х мерной бутылкой Клейна.
Фундаментальная группа такого многообразия:
![]() [20].
Здесь
[20].
Здесь
![]() - группа целых чисел. Это означает, что в таком пространстве есть 4 не
гомотопных пути, 3 из которых, при обходе по по замкнутому пути не меняют
ориентацию репера, а один - меняет ее на противоположную. Чтобы вернуть
ориентацию, необходимо пройти по этой петле дважды.
- группа целых чисел. Это означает, что в таком пространстве есть 4 не
гомотопных пути, 3 из которых, при обходе по по замкнутому пути не меняют
ориентацию репера, а один - меняет ее на противоположную. Чтобы вернуть
ориентацию, необходимо пройти по этой петле дважды.
Описанная топология фундаментальна, так как индуцируется фундаментальным отношением наблюдателя с остальной частью мира. Не трудно догадаться, что именно эта топология и ответственна за существование в природе двух сортов волновых функций – симметричных (переходящих в себя при перестановке двух любых частиц) и антисимметричных (меняющих знак при такой перестановке). В первом случае, как известно, частицы называются бозонами, во втором — фермионами.
Рассмотрим двухчастичную волновую функцию:
![]() .
При перестановке частиц, так как частицы тождественны, физическое состояние
системы не должно измениться. Это означает, что в общем случае, появится
фазовый множитель:
.
При перестановке частиц, так как частицы тождественны, физическое состояние
системы не должно измениться. Это означает, что в общем случае, появится
фазовый множитель:
![]()
Вернем систему в исходное состояние, подействовав на нее еще раз перестановочным оператором:
![]()
Отсюда следует, что
![]() и, поэтому
и, поэтому
![]() ;
;
![]() .
То есть волновая функция пары частиц может быть либо симметричной
либо антисимметричной:
.
То есть волновая функция пары частиц может быть либо симметричной
либо антисимметричной:
![]()
То есть, при перестановке частиц фаза изменяется либо на
![]() либо на
либо на
![]() .
На первый взгляд это странно, ибо перестановка частиц топологически всегда
должна приводить к кинку - топологической скрутке на
.
На первый взгляд это странно, ибо перестановка частиц топологически всегда
должна приводить к кинку - топологической скрутке на
![]() .
(Напомним, что сдвиг фазы на
.
(Напомним, что сдвиг фазы на
![]() мы интерпретируем, как перемещение вдоль петли длиной L на расстояние
мы интерпретируем, как перемещение вдоль петли длиной L на расстояние
![]() ).
Не трудно догадаться, что частицы, которые ведут себя по первому сценарию
(фаза изменяется на
).
Не трудно догадаться, что частицы, которые ведут себя по первому сценарию
(фаза изменяется на
![]() )
являются бозонами. Это те частицы, которые двигаясь по ориентируемым путям
(назовем бозонной степенью свободы) на бутылке Клейна и делая круг вдоль петли,
возвращаются в исходную точку с первоначальной фазой. Второй сценарий
соответствует движению по неориентируемому пути (фермионная степень свободы).
Поэтому пространственный поворот на
)
являются бозонами. Это те частицы, которые двигаясь по ориентируемым путям
(назовем бозонной степенью свободы) на бутылке Клейна и делая круг вдоль петли,
возвращаются в исходную точку с первоначальной фазой. Второй сценарий
соответствует движению по неориентируемому пути (фермионная степень свободы).
Поэтому пространственный поворот на
![]() это только половина пути по петле, длина которой в 2 раза больше (дважды
накрывающая топология). То есть при пространственном повороте на
это только половина пути по петле, длина которой в 2 раза больше (дважды
накрывающая топология). То есть при пространственном повороте на
![]() ,
фаза волновой функции меняется только на
,
фаза волновой функции меняется только на
![]() .
Этот сценарий соответствует поведению фермионов.
.
Этот сценарий соответствует поведению фермионов.
Антисимметричную функцию всегда можно записать следующим образом:
![]()
Где
![]() - состояния электронов. При
- состояния электронов. При
![]() очевидно
очевидно
![]() .
То есть ни какие 2 фермиона не могут находится в одном и том же состоянии.
Это содержание принципа Паули. Здесь возможна красивая топологическая
интерпретация. Из фундаментальной группы бутылки Клейна
.
То есть ни какие 2 фермиона не могут находится в одном и том же состоянии.
Это содержание принципа Паули. Здесь возможна красивая топологическая
интерпретация. Из фундаментальной группы бутылки Клейна
![]() следует, что на бозонные степени свободы мы можем намотать сколько угодно
витков, а на фермионную только один виток. Каждый второй виток
"соскальзывает" при намотке по этому пути. Достаточно бумаги и
карандаша чтобы проверить, как это работает на
следует, что на бозонные степени свободы мы можем намотать сколько угодно
витков, а на фермионную только один виток. Каждый второй виток
"соскальзывает" при намотке по этому пути. Достаточно бумаги и
карандаша чтобы проверить, как это работает на
![]() .
Сделайте это красивое упражнение! Теперь, если мы предположим, что каждый
виток представляет частицу, то принцип Паули следует из топологической
невозможности "намотать" на фермионную степень свободы более одного
витка. Если бы физическое пространство было сферой, то в таком мире не было бы
ни одной частицы. Это следствие того, что ее фундаментальная группа тривиальна
.
Сделайте это красивое упражнение! Теперь, если мы предположим, что каждый
виток представляет частицу, то принцип Паули следует из топологической
невозможности "намотать" на фермионную степень свободы более одного
витка. Если бы физическое пространство было сферой, то в таком мире не было бы
ни одной частицы. Это следствие того, что ее фундаментальная группа тривиальна
![]() .
И любая петля стягивается в точку (соскальзывает). Если бы физическое
пространство было тором с фундаментальной группой
.
И любая петля стягивается в точку (соскальзывает). Если бы физическое
пространство было тором с фундаментальной группой
![]() ,
то в таком мире не существовало бы фермионов. Такой мир представлял бы собой
сверхплотный бозе конденсат, - что-то наподобие нейтронной звезды. А вот
проективные пространства занимают промежуточное место в такой классификации –
с них "соскальзывает" только каждый второй виток!
,
то в таком мире не существовало бы фермионов. Такой мир представлял бы собой
сверхплотный бозе конденсат, - что-то наподобие нейтронной звезды. А вот
проективные пространства занимают промежуточное место в такой классификации –
с них "соскальзывает" только каждый второй виток!
![]() .
Бутылка Клейна является представителем проективных пространств и комбинирует
в себе свойства тора и проективной плоскости. Это дает возможность
для существования, в нашем мире, как бозонов, так и фермионов и делает его
столь сложным и многообразным.
.
Бутылка Клейна является представителем проективных пространств и комбинирует
в себе свойства тора и проективной плоскости. Это дает возможность
для существования, в нашем мире, как бозонов, так и фермионов и делает его
столь сложным и многообразным.
Субъективный скейлинг и квантовые флуктуации
Переход от функции
![]() является естественным явлением, сопутствующим процессу измерения. Мы называем
его субъективным скейлингом (перемасштабированием). Этот процесс
лежит в основе квантовой редукции. Реально все процессы протекают
в объективном времени, но наблюдатель (субъект) живет в субъективном времени
является естественным явлением, сопутствующим процессу измерения. Мы называем
его субъективным скейлингом (перемасштабированием). Этот процесс
лежит в основе квантовой редукции. Реально все процессы протекают
в объективном времени, но наблюдатель (субъект) живет в субъективном времени
![]() .
Вследствие неполноты, для него возникает понятие скрытого времени, когда
каждый нулевой момент времени имеет конечную длительность.
.
Вследствие неполноты, для него возникает понятие скрытого времени, когда
каждый нулевой момент времени имеет конечную длительность.
Как мы видели, это позволяет легко интерпретировать нелокальные проявления квантовой механики.
Состояния, описываемые объективной функцией
![]() ,
не являются физическими ибо физические состояния мы определили, как состояния
самого наблюдателя. Каждое состояние наблюдателя (физическое состояние)
образует класс
,
не являются физическими ибо физические состояния мы определили, как состояния
самого наблюдателя. Каждое состояние наблюдателя (физическое состояние)
образует класс
![]() неразличимых (скрытых) состояний. Этот класс, как мы уже говорили,
отождествляется c группой U(1)
фазовых трансформаций
вектора состояния системы. Сделать такое отождествление позволяет нам,
взятая за основу, конечность множества состояний наблюдателя, где любая
функция неизбежно циклична.
неразличимых (скрытых) состояний. Этот класс, как мы уже говорили,
отождествляется c группой U(1)
фазовых трансформаций
вектора состояния системы. Сделать такое отождествление позволяет нам,
взятая за основу, конечность множества состояний наблюдателя, где любая
функция неизбежно циклична.
Так как для нас время вырождено, то в данный момент времени частица может
находится одновременно в разных местах траектории. И двигаться она может так
же с разными скоростями. Эти скорости (объективные) всегда кратны скорости
света. Действительно, пусть
δx
минимально различимый путь, а
δτ
- минимально различимое время. За время
δτ
частица может пройти любой путь, но обязана вернуться в окрестность
δx,
что требует условие непрерывности. Положим
![]() .
Допустим частица за время
δτ
проходит путь
.
Допустим частица за время
δτ
проходит путь
![]() .
(L всегда складывается из целого числа квантов
δx).
Тогда, объективная скорость равна
.
(L всегда складывается из целого числа квантов
δx).
Тогда, объективная скорость равна
![]() .
И наконец, если опять же, учесть, что частица, двигаясь по петле, со скоростью
nc возвращается в окрестность исходной точки, то частота петлевого осциллятора
составит:
.
И наконец, если опять же, учесть, что частица, двигаясь по петле, со скоростью
nc возвращается в окрестность исходной точки, то частота петлевого осциллятора
составит:
![]() .
Итак, движение частицы описывается суперпозицией
ξ
ортогональных функций:
.
Итак, движение частицы описывается суперпозицией
ξ
ортогональных функций:
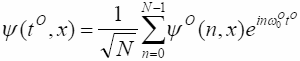 (48)
(48)
![]() - либо есть частица, либо нет.
- либо есть частица, либо нет.
Субъективная (относящаяся к субъекту) часть
![]() мировой функции
мировой функции
![]() уже не будет эргодической и ее значения на области
уже не будет эргодической и ее значения на области
![]() неизбежно повторяются с периодом
неизбежно повторяются с периодом
![]() .
Так как состояния в каждом цикле идентичны, это означает, что для физического
наблюдателя значимым будет только период времени
.
Так как состояния в каждом цикле идентичны, это означает, что для физического
наблюдателя значимым будет только период времени
![]() .
То есть при переходе к физической (наблюдаемой) картине мира, мы должны
перемасштабировать время
.
То есть при переходе к физической (наблюдаемой) картине мира, мы должны
перемасштабировать время
![]() .
Формально, переход к субъективному наблюдателю является редукцией к
пространству меньшей размерности. Такой переход приводит к перколяции
в пространстве частот. Мы должны сгруппировать в (48) члены суммы с близкими
частотами неразличимыми субъектом. Критерий неразличимости:
.
Формально, переход к субъективному наблюдателю является редукцией к
пространству меньшей размерности. Такой переход приводит к перколяции
в пространстве частот. Мы должны сгруппировать в (48) члены суммы с близкими
частотами неразличимыми субъектом. Критерий неразличимости:
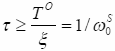 .
Новый редуцированный базис, полученный после перенормировки есть ничто иное,
как базис Гильбертова пространства физических состояний.
Разложение по физическому базису:
.
Новый редуцированный базис, полученный после перенормировки есть ничто иное,
как базис Гильбертова пространства физических состояний.
Разложение по физическому базису:
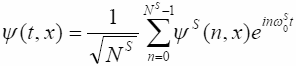 (49)
(49)
Здесь уже идет суммирование по хорошо различимым - квантовым состояниям
с весовыми множителями
![]() ,
определенными количеством элементов в кластерах частот, или, как мы показали
выше, числом ненулевых проекций из соответствующего бинарного пространства
состояний на вектор физического состояния.
,
определенными количеством элементов в кластерах частот, или, как мы показали
выше, числом ненулевых проекций из соответствующего бинарного пространства
состояний на вектор физического состояния.
Мы можем легко определить вероятность физического состояния,
как неотрицательную аддитивную нормированную меру, заданную над Булевой
σ-алгеброй [21] классов объективных состояний (В традиционной
σ-алгебре это – события £ на множестве элементарных исходов Ω).
Учитывая, евклидовость метрики Фурье, а так же то, что коэффициенты мы
определили на двоичном поле
![]() ,
вероятностная мера может быть определена, как мощность класса объективных
состояний. Действительно,
,
вероятностная мера может быть определена, как мощность класса объективных
состояний. Действительно,
![]() , где
ξ(x)- степень вырождения состояния "x". При этом проекционный
постулат фон-Неймана, описывающий переход к вероятностям, становится очевидным
следствием модели. Действительно, вероятность определяется просто степенью
вырождения данного физического состояния и вычисляется, как скалярное
произведение
, где
ξ(x)- степень вырождения состояния "x". При этом проекционный
постулат фон-Неймана, описывающий переход к вероятностям, становится очевидным
следствием модели. Действительно, вероятность определяется просто степенью
вырождения данного физического состояния и вычисляется, как скалярное
произведение
![]() .
.
Таким образом, переход к субъективному наблюдателю описывается перемасштабированием времени, и приводит к тому, что единый алгоритмический процесс распадается на неразличимые циклы (процессы), составляющие "вес" или "амплитуду" квантового состояния (переход от (48)→(49)). В КМ аргументом комплексных чисел кодируются степени вырождения, а фаза, как мы показали, может интерпретироваться чисто кинематически, как фаза циклического процесса, например, движения частицы в скрытом времени.
Вследствие перенормировки, единый цикл объективно-детерминированного движения частицы, распадается на ряд не связанных (с точки зрения субъективного наблюдателя) циклов с разными (субъективно неразличимыми) фазами. Возникает поле частиц двойников. При измерении, когда одна из частиц пакета попадает в «капкан» детектора, весь пакет «схлопывается», так как на объективном уровне реальности имеет место всего одна частица, совершающая циклическое движение. При этом наблюдатель осознает себя (случайно с его точки зрения) в одной из Эвереттовских эпох. Квантовая теория постулирует процесс редукции, оставляя механизм явления за пределами рассмотрения.
Выводы и обсуждение
В завершение мы предлагаем читателю скелет логических выводов, который мог остаться не замеченным за текстом и который может служить основой, проектом будущей теории субъективной физики.
В основу субъективной физики положены 2 основные аксиомы. Первая аксиома основополагающая:
Аксиома 1. Физические состояния мира являются состояниями сознания.
Вторая - конструктивная аксиома. Она определяет базу для всего построения:
Аксиома 2. Мир конечен и субъект (наблюдатель) является его частью.
Здесь допустимы разные модели. Наиболее красива модель, в которой мир представляется отображением пространства состояний сознания в себя. Эта аксиома влечет за собой ряд важнейших следствий.
- Следствие 1. Состояния сознания вырождены (неполнота).
- Следствие 2. Состояния сознания образуют циклическую группу.
Из этих следствий, в свою очередь, вытекает:
A. Существование скрытого пространства-времени.
B. Нелокальность процессов на физическом плане реальности.
C. Цикличность основных процессов на фундаментальном уровне.
Эти выводы, в свою очередь, служат базой для обоснования квантовой механики.
- Следствие 3. Состояния сознания образуют фактор-группу.
Выводы из этого следствия:
A. Физическое пространство-время имеет проективную топологию.
B. Гильбертово пространство квантовых состояний, как фактор-пространство классов эквивалентности фазовых трансформаций вектора состояния, так же имеет проективную топологию.
C. Гильбертово пространство квантовой механики изоморфно пространству-времени релятивистской теории. То есть, Гильбертово пространство не является некоей абстрактной дополнительной сущностью. Любое квантовое состояние имеет свой пространственно-топологический эквивалент. То есть это одна и та же сущность - пространство состояний сознания.
В настоящей статье с позиции субъективной физики, фрагментарно, были рассмотрены некоторые проблемы из области квантовой и релятивисткой теорий. В параграфе 2 мы исследовали природу волновой функции. Мы показали, что волновая функция описывает поле траекторий в пространстве состояний сознания. Квантовая суперпозиция при этом описывается, как объединение множеств состояний сознания в скрытом времени. В этой концепции компоненты суперпозиции (Эвереттовские альтернативные миры) рассматриваются, как классы эквивалентности по группе состояний сознания. Понятия вероятности и выбора в настоящей концепции приобретают относительный характер. А именно, вероятностный процесс выбора альтернатив (при измерении) для субъекта, - полностью детерминирован на объективном уровне реальности. Проблема измерения в рассматриваемой концепции отсутствует. Любая точка в пространстве сознания является потенциальным актом измерения. В 6-ом параграфе рассмотрена известная в квантовой теории "проблема фазы". Показано, что переформулировка квантовой механики на полях Галуа эффективно снимает проблему. Понятие поля в субъективной физике вторично. Здесь мы говорим о полях траекторий в пространстве сознания. Поэтому, фаза понимается не как фаза колебаний поля, а как координата точки в фазовом пространстве сознания. В 10-ом параграфе в контексте модели субъективной физики рассматривается идея калибровочных симметрий и ее связь с моделью Калуцы-Клейна. Рассматривается происхождение классических понятий энергии, массы, заряда и действия. В 11 параграфе исследуется субъективное происхождение метрики Минковского и особенности топологии субъективного пространства. Показано, что существование двух сортов частиц - фермионов и бозонов обусловлено этой субъективно - индуцированной топологией.
Литература
1. А.В. Каминский. Наблюдатель во Вселенной. Квантовая Магия, том 7, вып. 2, стр. 2101-2117, 2010
2. Everett H. III, "Relative state" Formulation of Quantum Mechanics. Rev. Mod. Phys. 29, 454 (1957).
3. А.В. Каминский. Моделирование физики в условиях неполноты. Квантовая Магия, том 1, вып. 3, стр. 3126-3149, 2004
4. А.В. Каминский. Скрытое пространство-время в физике. Квантовая Магия, том 2, вып. 1, стр. 1101-1125, 2007
5. А.В. Каминский. Необратимость как свойство сознания. Квантовая Магия, том 7, вып. 4, стр. 4123-4131, 2010
6. А.В. Каминский. Что описывают волновые уравнения? Квантовая Магия, том 6, вып. 2, стр. 2101-2109, 2009
7. А.Н.Колмогоров. Упрощенное доказательство эргодической теоремы Биркгофа–Хинчина.
УМН, 1938, выпуск 5, страницы 52–56
8. Arnol'd V.I. Эргодические и арифметические свойства динамики и орбит геометрической прогрессии. Mosc. Math.J., 5:1 (2005), 5–222.
9. Картеси Ф. Введение в конечные геометрии. 1980
10. А.В. Каминский. Анатомия квантовой суперпозиции. Квантовая Магия, том 3, вып. 1, стр. 1130-1142, 2006
11. London F.Z. Phys. 37 915 (1926); 40 193 (1927).
12. Susskind L., Glogower J. -Physics, 1964, vol 1. P. 49.
13. В.И. Арнольд. "Математические методы классической механики", Эдиториал УРСС, М., 2000
14. К.А. Бронников, С.Г. Рубин. Лекции по гравитации и космологии. Учебное пособие. М.: МИФИ, 2008. 460 с.
15. О' Rаifеаrtaigh L., Lorentz invariance and internal symmetry, "Phys. Rev.", 1965, v. 139, p. B1052;
16. Цих А.К Многообразие геометрий. Соросовский Образовательный Журнал, №2, 1999. 122.
17. [D.Hilbert und S. Cohn-Vossen Anschauliche Geometrie. Berlin Verlag von J. Springer 1932. Перевод: math.ru/lib/ files/djvu/geometry/kon-fossen.djvu].
18. Richard P. Feynman and Steven Weinberg, Elementary Particles and the Laws of Physics: the 1986 Dirac Memorial Lectures, Cambridge U. Press, Cambridge, 1987.
19. John Baez, Michael Ody and Bill Richter, Topological aspects of spin and statistics of solitons in nonlinear sigma-models, Jour. Math. Phys. 36 (1995), 108-131.
20. Codimension Two Nonorientable Submanifolds with Nonnegative Curvature Yuriko Y. Baldin and Francesco Mercuri. Proceedings of the American Mathematical Society. Vol. 103, No. 3 (Jul., 1988), pp. 918-920
21. Колмогоров А.Н. Основные понятия теории вероятностей. М., ГНТИ, 1936.
[1] Исключение составляет модель соотнесенных состояний Эверетта [2].
[2]
Если l–простое, то группа образует поле. Пусть "α"
элемент группы, тогда
![]() где
где
![]() пробегает все элементы группы и, в частности, через ее 1. Значит, для любого
"α" есть обратный элемент
пробегает все элементы группы и, в частности, через ее 1. Значит, для любого
"α" есть обратный элемент
![]()
[3] Число субъективно-трансфинитно, если оно превосходит число состояний субъекта.
[4]
если оператор
![]() эрмитов,
то оператор
эрмитов,
то оператор
![]() унитарен.
унитарен.
[5] Тильдой обозначены субъективные значения. Субъективный 0 и субъективная бесконечность - конечные числа трансфинитные для конечного наблюдателя.
[6] Для большей части континуальной математики в дискретной математике находятся соответствующие аналоги. Так, например на полях Галуа справедливы те же самые операции, что и на непрерывном поле. Над конечными полями могут быть построены те же самые хорошо известные геометрии, как евклидовы так и неевклидовы. Для нас это важно, так как строгое обоснование выводов, которые мы делаем, может быть дано только в рамках конечной модели. При этом, возможно использование математического анализа и геометрии на континууме в качестве удобного приема, но не более.
Другие работы автора на сайте digitalphysics.ru
Каминский А.В. Этюды о неполноте // LAP Lambert Academic Publishing. 2016.